题目内容
14.已知a,b,c满足1+2a+a2+$\sqrt{{b^2}-4b+4}+\sqrt{a+b+c}$=0,那么a+2b-c=4.分析 利用配方法对等式的左边进行变形处理,然后由非负数的性质来求a、b、c的值,最后代入所求的代数式进行求值即可.
解答 解:∵a,b,c满足1+2a+a2+$\sqrt{{b^2}-4b+4}+\sqrt{a+b+c}$=0,
∴(a+1)2+|b-2|+$\sqrt{a+b+c}$=0,
则$\left\{\begin{array}{l}{a+1=0}\\{b-2=0}\\{a+b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=-1}\end{array}\right.$,
所以a+2b-c=-1+4+1=4.
故答案是:4.
点评 本题考查了配方法的应用,非负数的性质.掌握完全平方公式是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列事件中,必然事件的是( )
| A. | a是实数,-a2≤0 | |
| B. | 天上打雷后就下雨 | |
| C. | 掷一枚质地均匀的硬币一次,反面朝上 | |
| D. | 某运动员跳高的最好成绩是200.1米 |
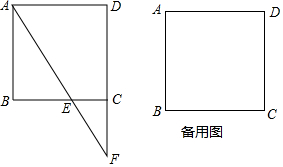 已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连结AE交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B1处.
已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连结AE交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B1处.