题目内容
在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=6cm,那么D点到直线AB的距离是 cm.
考点:角平分线的性质
专题:
分析:根据题意画出图形,再根据角平分线的性质即可得出结论.
解答: 解:如图所示,过点D作DE⊥AB于点E,
解:如图所示,过点D作DE⊥AB于点E,
∵在△ABC中,∠C=90°,AD平分∠CAB,
∴CD=DE.
∵BC=8cm,BD=6cm,
∴CD=8-6=2cm.
故答案为:2.
 解:如图所示,过点D作DE⊥AB于点E,
解:如图所示,过点D作DE⊥AB于点E,∵在△ABC中,∠C=90°,AD平分∠CAB,
∴CD=DE.
∵BC=8cm,BD=6cm,
∴CD=8-6=2cm.
故答案为:2.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
等腰三角形的两边分别为2cm,5cm,那么等腰三角形的周长为( )cm.
| A、9 | B、9或12 |
| C、12 | D、无法确定 |
若3a2-a-2=0,则5+2a-6a2=( )
| A、1 | B、-1 | C、9 | D、-9 |
0.1252008×(-8)2007的结果是( )
| A、0.125 | B、-0.125 |
| C、1 | D、-1 |
下列说法正确的是( )
| A、0.720有两个有效数字 |
| B、3.6万精确到十分位 |
| C、3.5×106精确到十分位 |
| D、5.078精确到0.001 |
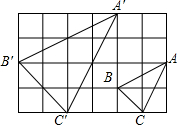 如图,由24个边长为1的正方形组成4×6的网格,若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是
如图,由24个边长为1的正方形组成4×6的网格,若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是