题目内容
下列变形正确的有( )
| A、由x-5=4x+2,可得x-4x=5+2 |
| B、由7x=4x-3,可得7x-4x=3 |
| C、由10x=11x-2,可得10x+11x=-2 |
| D、由5+x=12,可得x=12+5. |
考点:等式的性质
专题:
分析:根据等式的性质,等式的两边同时加上或减去同一个数或字母,等式仍成立;等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立,可得答案.
解答:解:A、两边都加(5-4x),故A正确;
B、左边减4x,右边减(4x-6),故B错误;
C、左边加11x,右边减11x,故C错误;
D、左边减5,右边加5,故D错误;
故选:A.
B、左边减4x,右边减(4x-6),故B错误;
C、左边加11x,右边减11x,故C错误;
D、左边减5,右边加5,故D错误;
故选:A.
点评:本题主要考查了等式的基本性质,等式的两边同时加上或减去同一个数或字母,等式仍成立;等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
下列由左到右的变形,属于因式分解的是( )
| A、m2-4=(m-2)(m+2) |
| B、(a+3)(a-3)=a2-9 |
| C、t2-16-6t=(t+4)(t-4)-6t |
| D、(m-2)(m-3)=(2-m)(3-m) |
0.1252008×(-8)2007的结果是( )
| A、0.125 | B、-0.125 |
| C、1 | D、-1 |
x3m+1可以写成( )
| A、(x3)m+1 |
| B、(xm)3+1 |
| C、xm3•x |
| D、(xm)3•x |
若x2-mx-15=(x+3)(x+n),则m、n的值分别为( )
| A、m=-2,n=5 |
| B、m=2,n=-5 |
| C、m=2,n=5 |
| D、m=-2,n=-5 |
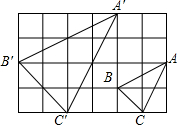 如图,由24个边长为1的正方形组成4×6的网格,若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是
如图,由24个边长为1的正方形组成4×6的网格,若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是