题目内容
6. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是56cm2,AB=20cm,AC=8cm,求DE的长.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是56cm2,AB=20cm,AC=8cm,求DE的长.
分析 根据角平分线性质得出DE=DF,根据三角形面积公式求出即可.
解答 解:∵AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∵△ABC面积是56cm2,AB=20cm,AC=8cm,
∴$\frac{1}{2}$×AB×DE+$\frac{1}{2}$×AC×DF=56cm2,
∴$\frac{1}{2}$×20×DE+$\frac{1}{2}$×8×DF=56cm2,
∴DE=DF=2cm.
点评 本题考查了角平分线性质的应用,能根据角平分线性质得出DE=DF是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
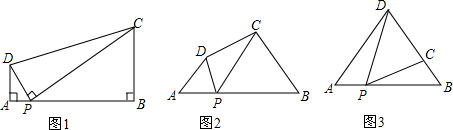
 如图,AC,BD相交于O,AB∥DC,∠D=40°,∠A=35°,则∠BOC=75°.
如图,AC,BD相交于O,AB∥DC,∠D=40°,∠A=35°,则∠BOC=75°.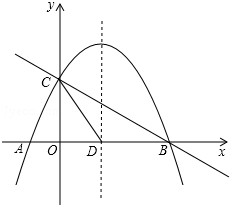 如图,抛物线y=-x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1,0),C(0,3)
如图,抛物线y=-x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1,0),C(0,3)