题目内容
计算:
(1)-22+20-|-3|×(-3)-1-(-0.2)2003×52002;
(2)(2a+3b)2-4a(a+3b+1)-(2a-b)(2a+b)-(a-3b)2;
(3)(-ab2)3•(-9a3b)÷(-3a3b5);
(4)已知:2m=3,4n=8,求:23m-2n+3的值;
(5)解关于x的方程:(x+2)2-(x-2)(x+2)=2;
(6)已知x2+3x-1=0,求:x3+5x2+5x+18的值.
(1)-22+20-|-3|×(-3)-1-(-0.2)2003×52002;
(2)(2a+3b)2-4a(a+3b+1)-(2a-b)(2a+b)-(a-3b)2;
(3)(-ab2)3•(-9a3b)÷(-3a3b5);
(4)已知:2m=3,4n=8,求:23m-2n+3的值;
(5)解关于x的方程:(x+2)2-(x-2)(x+2)=2;
(6)已知x2+3x-1=0,求:x3+5x2+5x+18的值.
考点:整式的混合运算
专题:计算题
分析:(1)原式第一项利用乘方的意义化简,第二项利用零指数幂法则计算,第三项利用绝对值的意义及负指数幂法则计算,最后一项逆用积的乘方运算法则计算即可得到结果;
(2)原式利用完全平方公式,平方差公式,以及单项式乘以多项式法则计算,去括号合并即可得到结果;
(3)原式利用单项式乘除单项式法则计算即可得到结果;
(4)原式变形后,将已知等式代入计算即可求出值;
(5)方程去括号,移项合并,将x系数化为1,即可求出解;
(6)已知等式变形后代入计算即可求出值.
(2)原式利用完全平方公式,平方差公式,以及单项式乘以多项式法则计算,去括号合并即可得到结果;
(3)原式利用单项式乘除单项式法则计算即可得到结果;
(4)原式变形后,将已知等式代入计算即可求出值;
(5)方程去括号,移项合并,将x系数化为1,即可求出解;
(6)已知等式变形后代入计算即可求出值.
解答:解:(1)原式=-4+1+1+0.2=-1.8;
(2)原式=4a2+12ab+9b2-4a2-12ab-4a-4a2+b2-a2+6ab-9b2=-5a2+b2-4a+6ab;
(3)原式=(-a3b6)•(-9a3b)÷(-3a3b5)=-3a3b2;
(4)∵2m=3,4n=8,
∴23m-2n+3=(2m)3÷(4n)×23=27÷8×8=27;
(5)去括号得:x2+4x+4-x2+4=2,
移项合并得:4x=-6,
解得:x=-1.5;
(6)∵x2+3x-1=0,即x2=1-3x,
∴原式=x(1-3x)+5(1-3x)+5x+18=x-3x2+5-15x+5x+18=-3(1-3x)-9x+23=-3+9x-9x+23=20.
(2)原式=4a2+12ab+9b2-4a2-12ab-4a-4a2+b2-a2+6ab-9b2=-5a2+b2-4a+6ab;
(3)原式=(-a3b6)•(-9a3b)÷(-3a3b5)=-3a3b2;
(4)∵2m=3,4n=8,
∴23m-2n+3=(2m)3÷(4n)×23=27÷8×8=27;
(5)去括号得:x2+4x+4-x2+4=2,
移项合并得:4x=-6,
解得:x=-1.5;
(6)∵x2+3x-1=0,即x2=1-3x,
∴原式=x(1-3x)+5(1-3x)+5x+18=x-3x2+5-15x+5x+18=-3(1-3x)-9x+23=-3+9x-9x+23=20.
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个矩形的长和宽分别是3
、2
,则它的面积是( )
| 6 |
| 3 |
A、20
| ||
B、18
| ||
C、17
| ||
D、16
|
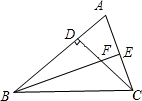 在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,并于CD相交于点F.
在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,并于CD相交于点F.