题目内容
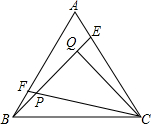 如图,点E,F分别是正△ABC的边AC,AB上的点,AE=BF,BE,CF相交于点P,CQ⊥BE于Q,若PF=1,PQ=3,则BE=
如图,点E,F分别是正△ABC的边AC,AB上的点,AE=BF,BE,CF相交于点P,CQ⊥BE于Q,若PF=1,PQ=3,则BE=考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:如图,证明△ABE≌△BCF,得到BE=CF;证明∠QPC=60°,此为解题的关键性结论;证明PC=2PQ=6,即可解决问题.
解答: 解:如图,∵△ABC为等边三角形,
解:如图,∵△ABC为等边三角形,
∴AB=BC,∠A=∠FBC=60°;
在△ABE与△BCF中,
,
∴△ABE≌△BCF(SAS),
∴BE=CF;∠FBP=∠BCP,
∴∠QPC=∠PBC+∠BCP
=∠PBC+∠FBP=∠FBC=60°;
∵CQ⊥PQ,
∴∠PCQ=30°,PC=2PQ=6,
∴BE=CF=6+1=7,
故答案为7.
 解:如图,∵△ABC为等边三角形,
解:如图,∵△ABC为等边三角形,∴AB=BC,∠A=∠FBC=60°;
在△ABE与△BCF中,
|
∴△ABE≌△BCF(SAS),
∴BE=CF;∠FBP=∠BCP,
∴∠QPC=∠PBC+∠BCP
=∠PBC+∠FBP=∠FBC=60°;
∵CQ⊥PQ,
∴∠PCQ=30°,PC=2PQ=6,
∴BE=CF=6+1=7,
故答案为7.
点评:该题主要考查了等边三角形的性质、全等三角形的判定及其性质的应用等几何知识点问题;解题的关键是数形结合,准确找出图形中隐含的相等或全等关系.

练习册系列答案
相关题目
 如图,点C的射线AB上,点D为线段BC的中点,已知AB=4,以C为端点的所有线段之和为9,求线段BD的长.
如图,点C的射线AB上,点D为线段BC的中点,已知AB=4,以C为端点的所有线段之和为9,求线段BD的长.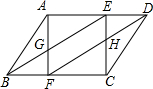 如图,在?ABCD中,点E、F分别是AD、BC上的点,且DE=BF,你能判断四边形GFHE的形状吗?请你说明理由.
如图,在?ABCD中,点E、F分别是AD、BC上的点,且DE=BF,你能判断四边形GFHE的形状吗?请你说明理由. 如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1m,球路的最高点B(8,9),则:
如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1m,球路的最高点B(8,9),则: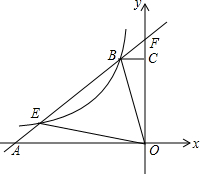 如图,直角梯形OABC的腰OC在y轴的正半轴上,点A(5n,0)在x轴的负半轴上,OA:AB:OC=5:5:3.点D是线段OC上一点,且OD=BD.
如图,直角梯形OABC的腰OC在y轴的正半轴上,点A(5n,0)在x轴的负半轴上,OA:AB:OC=5:5:3.点D是线段OC上一点,且OD=BD.