题目内容
 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.(1)求证:DE是⊙O的切线.
(2)若AB=30,AE=24,求AC的长.
考点:切线的判定
专题:
分析:(1)连接OC,由条件可得到∠OCA=∠EAC,可证明OC∥AE,可得到OC⊥DE,可证明DE是⊙O的切线;
(2)由条件可证明△AEC∽△ACB,可求得AC.
(2)由条件可证明△AEC∽△ACB,可求得AC.
解答:(1)证明:如图,连接OC,
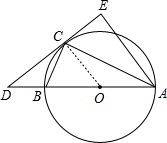
∵OA=OC,
∴∠BAC=∠OCA,
又∵AC平分∠EAB,
∴∠BAC=∠EAC,
∴∠OCA=∠EAC,
∴OC∥AE,且AE⊥DC
∴∠E=∠DCO=90°,
∴OC⊥CD,
∴CD为⊙O的切线;
(2)解:∵AB为⊙O的直径,
∴∠BCA=∠E=90°,且∠EAC=∠CAB,
∴△EAC∽△CAB,
∴
=
,即
=
,
解得AC=12
.

∵OA=OC,
∴∠BAC=∠OCA,
又∵AC平分∠EAB,
∴∠BAC=∠EAC,
∴∠OCA=∠EAC,
∴OC∥AE,且AE⊥DC
∴∠E=∠DCO=90°,
∴OC⊥CD,
∴CD为⊙O的切线;
(2)解:∵AB为⊙O的直径,
∴∠BCA=∠E=90°,且∠EAC=∠CAB,
∴△EAC∽△CAB,
∴
| AE |
| AC |
| AC |
| AB |
| 24 |
| AC |
| AC |
| 30 |
解得AC=12
| 5 |
点评:本题主要考查切线的判定及相似三角形的判定和性质,在证明切线时注意两种解题的思路,当有切点时,连接圆心和切点,证明垂直,当没有切点时,作垂直,证明距离等于半径,在解决有关线段的长度时,也可以利用相似三角形的对应边的比相等来求.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
如图所示,各正方体的四个数之间有相同的规律,根据此规律,“ ”位置的数是( )
”位置的数是( )

 ”位置的数是( )
”位置的数是( )
| A、144 | B、132 |
| C、168 | D、158 |
30°角的余角的补角是( )
| A、60° | B、150° |
| C、120° | D、不能确定 |
若等腰三角形的两内角度数比为1:4,则它的顶角为( )度.
| A、36或144 | B、20或120 |
| C、120 | D、20 |
 如图,已知△ABC中,∠A=75°,则∠1+∠2=( )
如图,已知△ABC中,∠A=75°,则∠1+∠2=( )| A、335° | B、255° |
| C、155° | D、150° |
 如图,点C的射线AB上,点D为线段BC的中点,已知AB=4,以C为端点的所有线段之和为9,求线段BD的长.
如图,点C的射线AB上,点D为线段BC的中点,已知AB=4,以C为端点的所有线段之和为9,求线段BD的长.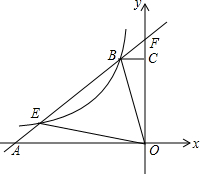 如图,直角梯形OABC的腰OC在y轴的正半轴上,点A(5n,0)在x轴的负半轴上,OA:AB:OC=5:5:3.点D是线段OC上一点,且OD=BD.
如图,直角梯形OABC的腰OC在y轴的正半轴上,点A(5n,0)在x轴的负半轴上,OA:AB:OC=5:5:3.点D是线段OC上一点,且OD=BD. 如图,点C在AB上,点M、N分别是AC、BC的中点,
如图,点C在AB上,点M、N分别是AC、BC的中点,