题目内容
15. 我国古代数学家赵爽的《勾股方圆图》是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图),如果大正方形的面积是16,小正方形的面积是3,直角三角形较短的直角边为a,较长的直角边为b那么(a+b)2的值为( )
我国古代数学家赵爽的《勾股方圆图》是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图),如果大正方形的面积是16,小正方形的面积是3,直角三角形较短的直角边为a,较长的直角边为b那么(a+b)2的值为( )| A. | 16 | B. | 29 | C. | 19 | D. | 48 |
分析 易求得ab的值,和a2+b2的值,根据完全平方公式即可求得(a+b)2的值,即可解题.
解答 解:∵大正方形的面积是16,小正方形的面积是3,
∴四个直角三角形面积和为16-3=13,即4×$\frac{1}{2}$ab=13,
∴2ab=13,a2+b2=16,
∴(a+b)2=a2+b2+2ab=16+13=29.
答:(a+b)2的值为29,
故选B.
点评 本题考查了完全平方公式的应用,考查了直角三角形中勾股定理的运用,本题中求得ab的值是解题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
6.已知点A(4,y1),B($\sqrt{2}$,y2),C(-2,y3)都在二次函数y=-2x2的图象上,则y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y2>y3>y1 | C. | y3>y2>y1 | D. | y2>y1>y3 |
10. 如图所示的正方体,如果把它展开,可以得到( )
如图所示的正方体,如果把它展开,可以得到( )
 如图所示的正方体,如果把它展开,可以得到( )
如图所示的正方体,如果把它展开,可以得到( )| A. |  | B. |  | C. |  | D. |  |
 如图,某小区规划在一个长20米、宽10米的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为27平方米,那么通道的宽应设计成多少米?
如图,某小区规划在一个长20米、宽10米的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为27平方米,那么通道的宽应设计成多少米?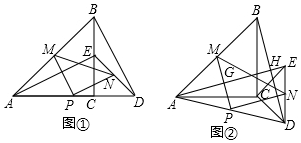
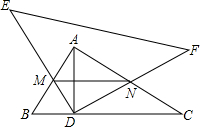 如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,AD是BC边上的高,以D为直角顶点的Rt△DEF绕点旋转,在旋转过程中,DE、EF分别与边AB、AC交于点M、N,则线段MN的最大值与最小值的差为$\frac{16}{5}$.
如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,AD是BC边上的高,以D为直角顶点的Rt△DEF绕点旋转,在旋转过程中,DE、EF分别与边AB、AC交于点M、N,则线段MN的最大值与最小值的差为$\frac{16}{5}$. 如图,在长为6m,宽为4m的矩形地面上修建两条宽均为1m的道路,余下部分做为耕地,根据图中数据,计算耕地面积为15m2.
如图,在长为6m,宽为4m的矩形地面上修建两条宽均为1m的道路,余下部分做为耕地,根据图中数据,计算耕地面积为15m2.