题目内容
11.用配方法解方程x2-4x-3=0,下列配方结果正确的是( )| A. | (x-2)2=7 | B. | (x-4)2=19 | C. | (x+2)2=7 | D. | (x+4)2=19 |
分析 先将常数项移至等式右边,再两边配上一次项系数一半的平方即可.
解答 解:x2-4x=3,
x2-4x+4=3+4,即(x-2)2=7,
故选:A.
点评 本题主要考查配方法解方程,用配方法解一元二次方程的步骤:①把原方程化为ax2+bx+c=0(a≠0)的形式;②方程两边同除以二次项系数,使二次项系数为1,并把常数项移到方程右边;③方程两边同时加上一次项系数一半的平方;④把左边配成一个完全平方式,右边化为一个常数;⑤如果右边是非负数,就可以进一步通过直接开平方法来求出它的解,如果右边是一个负数,则判定此方程无实数解.

练习册系列答案
相关题目
2.能说明命题“对于任何实数a,|a|>-a”是假命题的一个反例可以是( )
| A. | a=$\frac{1}{3}$ | B. | a=-2 | C. | a=1 | D. | a=$\sqrt{2}$ |
6.下列各对数中,数值相等的数是( )
| A. | -|23|与|-23| | B. | -32与(-3)2 | C. | (3×2)3与3×23 | D. | -23与(-2)3 |
3.在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1,若点B的坐标为(2,1),则点B的对应点B1的坐标为( )
| A. | (-2,-1) | B. | (2,-1) | C. | (-2,1) | D. | (1,2) |
20.某商店出售三种不同品牌的大米,米袋上分别标有质量,如表:
现从中任意拿出两袋不同品牌的大米,这两袋大米的质量最多相差( )
| 大米种类 | A品牌大米 | B品牌大米 | C品牌大米 |
| 质量标示 | (10±0.5)kg | (10±0.3)kg | (10±0.2)kg |
| A. | 0.8kg | B. | 0.6kg | C. | 0.4kg | D. | 0.5kg |
1. 如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5cm,则EF的长为( )
如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5cm,则EF的长为( )
 如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5cm,则EF的长为( )
如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5cm,则EF的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
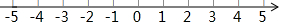 数轴如图所示,若点A,B在数轴上,点A与原点的距离为1个单位长度,点B与点A相距2个单位长度,则满足条件的所有点B与原点的距离的和是( )
数轴如图所示,若点A,B在数轴上,点A与原点的距离为1个单位长度,点B与点A相距2个单位长度,则满足条件的所有点B与原点的距离的和是( )