题目内容
12．
如图，直线AB∥CD，AC⊥AD，垂足为A，∠1=38°，则∠2的度数是（ ）| A． | 38° | B． | 42° | C． | 52° | D． | 62° |
分析 先根据AC⊥AD，∠1=38°，得出∠3，再根据平行线的性质，即可得到∠2的度数．
解答 
解：如图，∵AC⊥AD，∠1=38°，
∴∠3=90°-38°=52°，
∵AB∥CD，
∴∠2=∠3=52°，
故选：C．
点评 本题主要考查了平行线的性质，解题时注意：两直线平行，内错角相等．
练习册系列答案
相关题目
2．
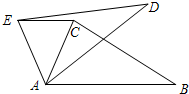如图在△ABC中，∠CAB=70°，在同一平面内，将△ABC绕点A逆时针旋转到△ADE的位置，使得EC∥AB，则∠CAE度数为（ ）
如图在△ABC中，∠CAB=70°，在同一平面内，将△ABC绕点A逆时针旋转到△ADE的位置，使得EC∥AB，则∠CAE度数为（ ）| A． | 30° | B． | 35° | C． | 40° | D． | 50° |
3．解分式方程$\frac{2}{x-1}$+$\frac{x+2}{1-x}$=1时，去分母变形后正确的是（ ）
| A． | 2-（x+2）=1 | B． | 2-x+2=x-1 | C． | 2-（x+2）=x-1 | D． | 2+（x+2）=x-1 |
20．
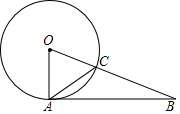如图，⊙O与AB相切于点A，BO与⊙O交于点C，∠BAC=30°，则∠B等于（ ）
如图，⊙O与AB相切于点A，BO与⊙O交于点C，∠BAC=30°，则∠B等于（ ）| A． | 20° | B． | 30° | C． | 50° | D． | 60° |
7．若关于x的不等式组$\left\{\begin{array}{l}{2x-3＜4x+5}\\{x-a＞1}\end{array}\right.$的解集是x＞-4，则a的取值范围是（ ）
| A． | a＞-4 | B． | a＜-5 | C． | a≥-5 | D． | a≤-5 |
4．已知正比例函数y=ax（a≠0）与反比例函数y=$\frac{k}{x}$（k≠0）图象的一个交点坐标为（-1，-1），则另一个交点坐标是（ ）
| A． | （1，-1） | B． | （1，1） | C． | （-1，1） | D． | （0，1） |
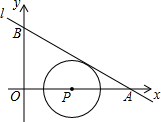我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y=kx+3$\sqrt{3}$与轴、轴分别交于A、B，∠OAB=30°，点P在轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是4．