题目内容
4.已知正比例函数y=ax(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)图象的一个交点坐标为(-1,-1),则另一个交点坐标是( )| A. | (1,-1) | B. | (1,1) | C. | (-1,1) | D. | (0,1) |
分析 首先求出两个函数的解析式,再利用方程组求交点坐标即可.
解答 解:∵正比例函数y=ax(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)图象的一个交点坐标为(-1,-1),
∴a=1,k=1,
∴正比例函数为y=x,反比例函数为y=$\frac{1}{x}$,
由$\left\{\begin{array}{l}{y=x}\\{y=\frac{1}{x}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$,
∴另一个交点坐标是(1,1),
故选B.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是熟练掌握待定系数法,学会利用方程组求交点坐标.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
15.一次函数y=kx+b的图象过原点和y=2x与x-y=1的交点,那么y=kx+b的解析式是( )
| A. | y=2x-1 | B. | y=2x+1 | C. | y=2x | D. | y=x |
12. 如图,直线AB∥CD,AC⊥AD,垂足为A,∠1=38°,则∠2的度数是( )
如图,直线AB∥CD,AC⊥AD,垂足为A,∠1=38°,则∠2的度数是( )
 如图,直线AB∥CD,AC⊥AD,垂足为A,∠1=38°,则∠2的度数是( )
如图,直线AB∥CD,AC⊥AD,垂足为A,∠1=38°,则∠2的度数是( )| A. | 38° | B. | 42° | C. | 52° | D. | 62° |
19.在$\frac{a-b}{2}$,$\frac{a+b}{a-b}$,$\frac{5+x}{π}$,3-$\frac{2}{x}$,$\frac{1}{4}$+y,(x-y)-1中,是分式的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
9. 如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=28,DE=4,AB=8,则AC=( )
如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=28,DE=4,AB=8,则AC=( )
 如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=28,DE=4,AB=8,则AC=( )
如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=28,DE=4,AB=8,则AC=( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
16.下列命题是真命题的是( )
| A. | 相等的角是对顶角 | |
| B. | 若实数a,b满足a2=b2,则a=b | |
| C. | 若实数a,b满足a<0,b<0,则ab<0 | |
| D. | 角的平分线上的点到角的两边的距离相等 |


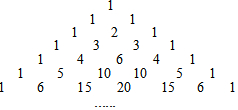 杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题:
杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题: