题目内容
2.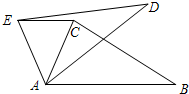 如图在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A逆时针旋转到△ADE的位置,使得EC∥AB,则∠CAE度数为( )
如图在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A逆时针旋转到△ADE的位置,使得EC∥AB,则∠CAE度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
分析 根据旋转的性质得AE=AC,∠BAD=∠EAC,再根据等腰三角形的性质得∠AEC=∠ACE,然后根据平行线的性质由CE∥AB得∠ACE=∠CAB=70°,则∠AEC=∠ACE=70°,再根据三角形内角和计算出∠CAE=40°即可.
解答 解:∵△ABC绕点A逆时针旋转到△AED的位置,
∴AE=AC,∠BAD=∠CAE,
∴∠ACE=∠AEC,
∵CE∥AB,
∴∠ACE=∠CAB=70°,
∴∠AEC=∠ACE=70°,
∴∠CAE=180°-2×70°=40°;
故选:C.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了平行线的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.点P(-2,1)关于y轴对称的点的坐标是( )
| A. | (-2,-1) | B. | (2,1) | C. | (2,-1) | D. | (-2,1) |
13. 如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
 如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )| A. | AB=CD | B. | EC=BF | C. | ∠A=∠D | D. | AB=BC |
10.下列运算正确的是( )
| A. | (-2a3)2=-4a6 | B. | $\sqrt{9}$=±3 | C. | m2•m3=m6 | D. | x5+2x5=3x5 |
17.下列运算正确的是( )
| A. | (-ab)2=-a2b2 | B. | (a+b)(a-b)=a2-b2 | C. | 3a2+2b=6a2b | D. | (a-b)2=a2+b2 |
7.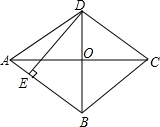 如图,菱形ABCD的对角线AC,BD交于点O,AC=8,BD=6,DE⊥AB于点E,则DE的长为( )
如图,菱形ABCD的对角线AC,BD交于点O,AC=8,BD=6,DE⊥AB于点E,则DE的长为( )
 如图,菱形ABCD的对角线AC,BD交于点O,AC=8,BD=6,DE⊥AB于点E,则DE的长为( )
如图,菱形ABCD的对角线AC,BD交于点O,AC=8,BD=6,DE⊥AB于点E,则DE的长为( )| A. | $\frac{12}{5}$ | B. | $\frac{24}{5}$ | C. | 6 | D. | 4 |
11.下列计算错误的是( )
| A. | $\sqrt{12}$÷$\sqrt{\frac{4}{3}}$=3 | B. | (1-$\sqrt{2}$)2=3-2$\sqrt{2}$ | C. | $\sqrt{(3-π)^{2}}$=3-π | D. | (-5$\sqrt{2}$+3$\sqrt{5}$)(-5$\sqrt{2}$-3$\sqrt{5}$)=5 |
12. 如图,直线AB∥CD,AC⊥AD,垂足为A,∠1=38°,则∠2的度数是( )
如图,直线AB∥CD,AC⊥AD,垂足为A,∠1=38°,则∠2的度数是( )
 如图,直线AB∥CD,AC⊥AD,垂足为A,∠1=38°,则∠2的度数是( )
如图,直线AB∥CD,AC⊥AD,垂足为A,∠1=38°,则∠2的度数是( )| A. | 38° | B. | 42° | C. | 52° | D. | 62° |