题目内容
13.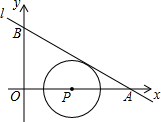 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+3$\sqrt{3}$与轴、轴分别交于A、B,∠OAB=30°,点P在轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是4.
我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+3$\sqrt{3}$与轴、轴分别交于A、B,∠OAB=30°,点P在轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是4.
分析 根据直线的解析式求得OB=3$\sqrt{3}$,进而求得OA=9,根据切线的性质求得PM⊥AB,根据∠OAB=30°,求得PM=$\frac{1}{2}$PA,然后根据“整圆”的定义,即可求得使得⊙P成为整圆的点P的坐标,从而求得点P个数.
解答 解:∵直线l:y=kx+3$\sqrt{3}$与x轴、y轴分别交于A、B,
∴B(0,3$\sqrt{3}$),
∴OB=3$\sqrt{3}$,
在Rt△AOB中,∠OAB=30°,
∴OA=$\sqrt{3}$OB=$\sqrt{3}$×3$\sqrt{3}$=9,
∵⊙P与l相切,设切点为M,连接PM,则PM⊥AB,
∴PM=$\frac{1}{2}$PA,
设P(x,0),
∴PA=9-x,
∴⊙P的半径PM=$\frac{1}{2}$PA=$\frac{9}{2}$-$\frac{1}{2}$x,
∵x为整数,PM为整数,
∴x可以取1,3,5,7,4个数,
∴使得⊙P成为整圆的点P个数是4.
故答案为4
点评 本题考查了切线的性质,含30°角的直角三角形的性质等,熟练掌握性质定理是解题的关键.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
12. 如图,直线AB∥CD,AC⊥AD,垂足为A,∠1=38°,则∠2的度数是( )
如图,直线AB∥CD,AC⊥AD,垂足为A,∠1=38°,则∠2的度数是( )
 如图,直线AB∥CD,AC⊥AD,垂足为A,∠1=38°,则∠2的度数是( )
如图,直线AB∥CD,AC⊥AD,垂足为A,∠1=38°,则∠2的度数是( )| A. | 38° | B. | 42° | C. | 52° | D. | 62° |
2.一辆小车由静止开始从光滑的斜面上向下滑动,通过观察记录小车滑动的距离s(m)与时间t(s)的数据如下表:
则写出用t表示s的关系式s=2t2.
| 时间t(s) | 1 | 2 | 3 | 4 | |
| 距离s(m) | 2 | 8 | 18 | 32 | … |
3.用平面去截一个立方体,截面不可能是( )
| A. | 正方形 | B. | 五边形 | C. | 六边形 | D. | 七边形 |
 在长方体ABCD-EFGH中,既与平面ADHE垂直,又与平面EFGH平行的平面是ABCD.
在长方体ABCD-EFGH中,既与平面ADHE垂直,又与平面EFGH平行的平面是ABCD.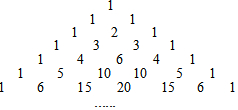 杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题:
杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题: