题目内容
5.已知$\frac{x}{2}=\frac{y}{3}=\frac{z}{4}$,则$\frac{x+y+z}{x-y-z}$的值为$-\frac{9}{5}$.分析 设$\frac{x}{2}=\frac{y}{3}=\frac{z}{4}$=$\frac{y}{3}$=$\frac{z}{4}$=k,则x=2k,y=3k,z=4k,然后代入所求的分式化简求值即可.
解答 解:设$\frac{x}{2}=\frac{y}{3}=\frac{z}{4}$=$\frac{y}{3}$=$\frac{z}{4}$=k,则x=2k,y=3k,z=4k,
∴原式=$\frac{2k+3k+4k}{2k-3k-4k}$=$-\frac{9}{5}$.
故答案为:-$\frac{9}{5}$.
点评 本题考查了分式的化简求值,正确设出未知数,利用k表示出x、y、z的值是关键.

练习册系列答案
相关题目
20.已知一次函数y1=k1x+b图象上的点A(t,m)和y2=k2x+b图象上的点B(t,n),且t>0,m<n,则k1与k2的大小关系是( )
| A. | k1<k2 | B. | k1=k2 | C. | k1>k2 | D. | 无法确定 |
17.点A(-4,a2+8)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
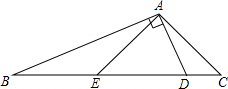 如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.若BD=13,则AC=6.5.
如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.若BD=13,则AC=6.5. 如图,在△ABC中,∠ACB=90°,D是AB的中点,CD=3,过点A作∠CAE=∠B,交边CB于点E,交线段CD于点H.
如图,在△ABC中,∠ACB=90°,D是AB的中点,CD=3,过点A作∠CAE=∠B,交边CB于点E,交线段CD于点H.