题目内容
16.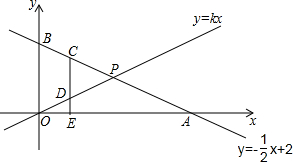 一次函数y=-$\frac{1}{2}$x+2的图象在平面直角坐标系中交x轴、y轴分别于A、B两点,交直线y=kx于P.
一次函数y=-$\frac{1}{2}$x+2的图象在平面直角坐标系中交x轴、y轴分别于A、B两点,交直线y=kx于P.(1)求点A、B的坐标;
(2)若OP=PA,求k的值;
(3)C是线段BP上一点,CE⊥x轴于E,交OP于D,若CD=2ED,求C点的坐标.
分析 (1)根据题意知,一次函数y=ax+b的图象过点B(0,2)和点A(4,0),把A、B代入求值即可;
(2)设P(x,y),根据PO=PA,列出方程,并与y=kx组成方程组,解方程组;
(3)设点C(x,-$\frac{1}{2}$x+2),再根据等量关系CD=2ED列方程求解.
解答 解:(1)当x=0时,y=-$\frac{1}{2}$x+2=2,
∴B(0,2)
当y=0时,y=-$\frac{1}{2}$x+2=0,
∴x=4,
∴A(4,0);
(2)设P(x,y),因为点P在直线y=-$\frac{1}{2}$x+2,
且OP=AP,
∴x=2,
把x=2代入y=-$\frac{1}{2}$x+2,y=1,所以点P的坐标是(2,1),
因为点P在直线y=kx上,所以k=$\frac{1}{2}$;
(3)设点C(x,-$\frac{1}{2}$x+2),则D(x,$\frac{1}{2}$x),E(x,0),
因为CD=2DE,所以-$\frac{1}{2}$x+2-$\frac{1}{2}$x=2×$\frac{1}{2}$x,
解得:x=1,则-$\frac{1}{2}$x+2=$\frac{3}{2}$,
所以点C的坐标为(1,$\frac{3}{2}$).
点评 本题要求利用图象求解各问题,要认真体会点的坐标,一次函数与一元一次方程组之间的内在联系.

练习册系列答案
相关题目
6.一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式:标准分=个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分高的考试成绩更好,请问A同学在本次考试中,数学、英语哪个学科考得更好?
| A | B | C | D | E | 平均分 | 标准差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 | $\sqrt{2}$ | |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 |
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式:标准分=个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分高的考试成绩更好,请问A同学在本次考试中,数学、英语哪个学科考得更好?
4.已知点M(3,-2),N(-3,-2),则直线MN与x轴、y轴的位置关系分别为( )
| A. | 相交,相交 | B. | 平行,平行 | C. | 垂直相交,平行 | D. | 平行,垂直相交 |
11.下列各组二次根式化简后,被开方数不相同的一组是( )
| A. | $\sqrt{0.3}$和$\sqrt{0.03}$ | B. | $\sqrt{\frac{2}{3}}$和$\sqrt{54}$ | C. | $\sqrt{12}$和$\sqrt{0.75}$ | D. | $\sqrt{\frac{4}{5}}$和$\sqrt{{2}^{2}+{4}^{2}}$ |
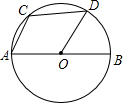 如图,已知AB是⊙O的直径,弦AC与半径OD平行.
如图,已知AB是⊙O的直径,弦AC与半径OD平行.