题目内容
8.已知$\sqrt{x}$+$\sqrt{y-1}$+$\sqrt{z-2}$=$\frac{1}{2}$(x+y+z),求xyz的值.分析 先利用配方法得到($\sqrt{x}$-1)2+($\sqrt{y-1}$-1)2+($\sqrt{z-2}$-1)2=0,再利用算术平方根的定义求出x、y、z.
解答 解:∵$\sqrt{x}$+$\sqrt{y-1}$+$\sqrt{z-2}$=$\frac{1}{2}$(x+y+z),
∴x-2$\sqrt{x}$+1+y-1-2$\sqrt{y-1}$+1+z-2-2$\sqrt{z-2}$+1=0,
∴($\sqrt{x}$-1)2+($\sqrt{y-1}$-1)2+($\sqrt{z-2}$-1)2=0,
∴$\sqrt{x}$-1=0,$\sqrt{y-1}$-1=0,$\sqrt{z-2}$-1=0,
∴x=1,y=2,z=3.
点评 本题考查了配方法的应用:用配方法解一元二次方程;利用配方法求二次三项式是一个完全平方式时所含字母系数的值.也考查了非负数的性质.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
18.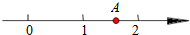 如图所示,在数轴上点A所表示的数x的范围是( )
如图所示,在数轴上点A所表示的数x的范围是( )
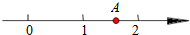 如图所示,在数轴上点A所表示的数x的范围是( )
如图所示,在数轴上点A所表示的数x的范围是( )| A. | $\frac{3}{2}$sin30°<x<sin60° | B. | cos30°<x<$\frac{3}{2}$cos45° | ||
| C. | $\frac{3}{2}$tan30°<x<tan45° | D. | $\frac{3}{2}$tan45°<x<tan60° |
 已知:如图,点A、E、F、C在同一直线上,∠A=∠C,AD=CB,AE=CF.
已知:如图,点A、E、F、C在同一直线上,∠A=∠C,AD=CB,AE=CF. 在如图所示的正方形网格里,以格点为顶点按要求画图,并回答问题.
在如图所示的正方形网格里,以格点为顶点按要求画图,并回答问题.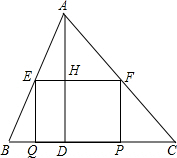 如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在边上,E、F两点分别在AB、AC上,AD交EF于点H.
如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在边上,E、F两点分别在AB、AC上,AD交EF于点H.