题目内容
3.已知关于x的方程$\frac{1}{2}$x2-2(1-k)x+2k-3=0的两根异号,则k的取值范围是k<$\frac{3}{2}$.分析 根据题意可得△>0,两根之积<0,解不等式组可求k的取值范围.
解答 解::∵方程有两个不相等的实数根,
∴△>0,
即4(1-k)2-2(2k-3)>0,
整理得:2(k-$\frac{3}{2}$)2+$\frac{1}{2}$>0,
∴k为任何数,
∵2(2k-3)<0,
解得:k<$\frac{3}{2}$.
故答案为:k<$\frac{3}{2}$.
点评 本题考查了根与系数的关系,解答本题的关键是掌握根的判别式以及两根之和为-$\frac{b}{a}$,两根之积为$\frac{c}{a}$.

练习册系列答案
相关题目
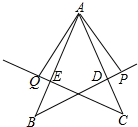 已知,如图,AB=AC,AD=AE,AP⊥BD,AQ⊥CE,垂足分别为P、Q,求证:AP=AQ.
已知,如图,AB=AC,AD=AE,AP⊥BD,AQ⊥CE,垂足分别为P、Q,求证:AP=AQ.