用换元法解方程$\frac{x^2-12}{x}$-$\frac{4x}{x^2-12}$=3时.设$\frac{x^2-12}{x}$=y.则原方程可化为( )A．y-$\frac{1}{y}$-3=0B．y-$\frac{4}{y}$-3=0C．y-$\frac{1}{y}$+3=0D．y-$\frac{4}{y}$+3=0 题目和参考答案——青夏教育精英家教网—

题目内容

17．用换元法解方程$\frac{x^2-12}{x}$-$\frac{4x}{x^2-12}$=3时，设$\frac{x^2-12}{x}$=y，则原方程可化为（　　）

A．

y-$\frac{1}{y}$-3=0

B．

y-$\frac{4}{y}$-3=0

C．

y-$\frac{1}{y}$+3=0

D．

y-$\frac{4}{y}$+3=0

分析直接利用已知将原式用y替换得出答案．

解答解：∵设$\frac{x^2-12}{x}$=y，
∴$\frac{x^2-12}{x}$-$\frac{4x}{x^2-12}$=3，可转化为：y-$\frac{4}{y}$=3，
即y-$\frac{4}{y}$-3=0．
故选：B．

点评此题主要考查了换元法解分式方程，正确得出y与x值间的关系是解题关键．

练习册系列答案

相关题目

7．

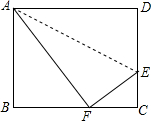如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知折痕AE=5$\sqrt{5}$cm，且tan∠EFC=$\frac{3}{4}$，那么矩形ABCD的周长为36cm．

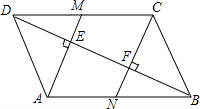8．已知关于x的一元二次方程x²+mx-8=0的一个实数根为2，则另一实数根及m的值分别为（　　）

5．

如图，?ABCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于M、N．
（1）求证：四边形CMAN是平行四边形．
（2）已知DE=4，FN=3，求BN的长．

12．

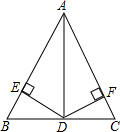如图，在△ABC中，AD平分∠BAC，且BD=CD，DE⊥AB于点E，DF⊥AC于点F．
（1）求证：AB=AC；
（2）若AD=2$\sqrt{3}$，∠DAC=30°，求AC的长．

2．

在综合实践课上，小聪所在小组要测量一条河的宽度，如图，河岸EF∥MN，小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向，然后沿河岸走了30米，到达B处，测得河对岸电线杆D位于北偏东30°方向，此时，其他同学测得CD=10米．请根据这些数据求出河的宽度为（30+10$\sqrt{3}$）米．（结果保留根号）

9．二次函数y=x²-2x+4化为y=a（x-h）²+k的形式，下列正确的是（　　）

6．已知二次函数y=ax²-2ax+c（a＜0）的最大值为4，且抛物线过点（$\frac{7}{2}$，-$\frac{9}{4}$），点P（t，0）是x轴上的动点，抛物线与y轴交点为C，顶点为D．
（1）求该二次函数的解析式，及顶点D的坐标；
（2）求|PC-PD|的最大值及对应的点P的坐标；
（3）设Q（0，2t）是y轴上的动点，若线段PQ与函数y=a|x|²-2a|x|+c的图象只有一个公共点，求t的取值．

8．某大学生利用业余时间参与了一家网店经营，销售一种成本为30元/件的文化衫，根据以往的销售经验，他整理出这种文化衫的售价y₁（元/件），销量y₂（件）与第x（1≤x＜90）天的函数图象如图所示（销售利润=（售价-成本）×销量）
（1）求y₁与y₂的函数表达式；
（2）求每天的销售利润w与x的函数关系表达式；
（3）销售这种文化衫的第多少天，每天销售利润最大，最大利润是多少？

试题分类