题目内容
12.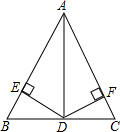 如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.(1)求证:AB=AC;
(2)若AD=2$\sqrt{3}$,∠DAC=30°,求AC的长.
分析 (1)先证明△DEB≌△DFC得∠B=∠C由此即可证明.
(2)先证明AD⊥BC,再在RT△ADC中,利用30°角性质设CD=a,AC=2a,根据勾股定理列出方程即可解决问题.
解答 (1)证明: ∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF,∠DEB=∠DFC=90°,
在RT△DEB和RT△DFC中,
$\left\{\begin{array}{l}{BD=DC}\\{DE=DF}\end{array}\right.$,
∴△DEB≌△DFC,
∴∠B=∠C,
∴AB=AC.
(2)∵AB=AC,BD=DC,
∴AD⊥BC,
在RT△ADC中,∵∠ADC=90°,AD=2$\sqrt{3}$,∠DAC=30°,
∴AC=2CD,设CD=a,则AC=2a,
∵AC2=AD2+CD2,
∴4a2=a2+(2$\sqrt{3}$)2,
∵a>0,
∴a=2,
∴AC=2a=4.
点评 本题考查全等三角形的判定和性质、直角三角形30°性质、勾股定理等知识,解题的关键是正确寻找全等三角形,记住直角三角形30°角所对的直角边等于斜边的一半,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.以下问题不适合全面调查的是( )
| A. | 调查某班学生每周课前预习的时间 | |
| B. | 调查某中学在职教师的身体健康状况 | |
| C. | 调查全国中小学生课外阅读情况 | |
| D. | 调查某校篮球队员的身高 |
17.用换元法解方程$\frac{x^2-12}{x}$-$\frac{4x}{x^2-12}$=3时,设$\frac{x^2-12}{x}$=y,则原方程可化为( )
| A. | y-$\frac{1}{y}$-3=0 | B. | y-$\frac{4}{y}$-3=0 | C. | y-$\frac{1}{y}$+3=0 | D. | y-$\frac{4}{y}$+3=0 |
 如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.
如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.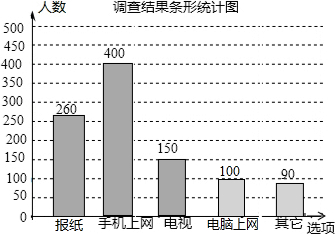 如图是某市电视台记者为了解市民获取新闻的主要图径,通过抽样调查绘制的一个条形统计图.若该市约有230万人,则可估计其中将报纸和手机上网作为获取新闻的主要途径的总人数大约为151.8万人.
如图是某市电视台记者为了解市民获取新闻的主要图径,通过抽样调查绘制的一个条形统计图.若该市约有230万人,则可估计其中将报纸和手机上网作为获取新闻的主要途径的总人数大约为151.8万人.