题目内容
8. 如图,△ABC的外角∠ACD的平分线与内角∠ABC的平分线交于点P,若∠BPC=41°,则∠CAP=50°.
如图,△ABC的外角∠ACD的平分线与内角∠ABC的平分线交于点P,若∠BPC=41°,则∠CAP=50°.
分析 根据外角与内角性质得出∠BAC的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP=∠FAP,即可得出答案.
解答 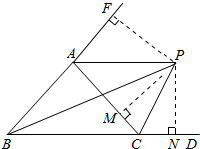 解:延长BA,作PN⊥BD,PF⊥BA,PM⊥AC,
解:延长BA,作PN⊥BD,PF⊥BA,PM⊥AC,
设∠PCD=x°,
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∵∠BPC=40°,
∴∠ABP=∠PBC=∠PCD-∠BPC=(x-40)°,
∴∠BAC=∠ACD-∠ABC=2x°-(x°-40°)-(x°-40°)=80°,
∴∠CAF=100°,
在Rt△PFA和Rt△PMA中,
∵$\left\{\begin{array}{l}{AP=PA}\\{PM=PF}\end{array}\right.$,
∴Rt△PFA≌Rt△PMA(HL),
∴∠FAP=∠PAC=50°.
故答案为:50°.
点评 此题主要考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识,根据角平分线的性质得出PM=PN=PF是解决问题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
19. 如图,小红用一个宽度相等的纸条按如图方法折叠一下,则∠1等于( )
如图,小红用一个宽度相等的纸条按如图方法折叠一下,则∠1等于( )
 如图,小红用一个宽度相等的纸条按如图方法折叠一下,则∠1等于( )
如图,小红用一个宽度相等的纸条按如图方法折叠一下,则∠1等于( )| A. | 40° | B. | 45° | C. | 56° | D. | 65° |
16.|-2017|的倒数是( )
| A. | -2017 | B. | 2017 | C. | $\frac{1}{2017}$ | D. | -$\frac{1}{2017}$ |
13.下列运算错误的是( )
| A. | a+2a=3a | B. | (a2)3=a6 | C. | a2•a3=a5 | D. | a6÷a3=a2 |
20.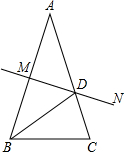 如图,AB=AC,AB的中垂线MN交AC于点D,交AB于点M,且BC=AD,下列结论中:①△BCD是等腰三角形;②BD平分∠ABC;③∠C=72°;④图中共有3个等腰三角形,其中正确的有( )
如图,AB=AC,AB的中垂线MN交AC于点D,交AB于点M,且BC=AD,下列结论中:①△BCD是等腰三角形;②BD平分∠ABC;③∠C=72°;④图中共有3个等腰三角形,其中正确的有( )
 如图,AB=AC,AB的中垂线MN交AC于点D,交AB于点M,且BC=AD,下列结论中:①△BCD是等腰三角形;②BD平分∠ABC;③∠C=72°;④图中共有3个等腰三角形,其中正确的有( )
如图,AB=AC,AB的中垂线MN交AC于点D,交AB于点M,且BC=AD,下列结论中:①△BCD是等腰三角形;②BD平分∠ABC;③∠C=72°;④图中共有3个等腰三角形,其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
17.一个五边形有三个内角是直角,另两个内角都等于n,则n的值是( )
| A. | 30° | B. | 120° | C. | 135° | D. | 108° |