题目内容
3．把m$\sqrt{-\frac{1}{m}}$化简后的结果为（ ）| A． | $\sqrt{m}$ | B． | -m | C． | -$\sqrt{m}$ | D． | -$\sqrt{-m}$ |
分析 根据二次根式的性质即可求出答案．
解答 解：由题意可知：-$\frac{1}{m}$＞0，
∴m＜0，
∴原式=m$\sqrt{\frac{1}{-m}}$=m$\sqrt{\frac{-m}{{m}^{2}}}$=m$\frac{\sqrt{-m}}{|m|}$=-$\sqrt{-m}$
故答案为：（D）
点评 本题考查二次根式的性质，解题的关键是熟练运用二次根式的性质，本题属于基础题型．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
1．小明为备战体育中考，每天早晨坚持锻炼，他花20分钟慢跑到离家900米的江边，在江边休息10分钟后，再用15分钟快跑回家，下列图中表示小明离家的距离y（米）与时间x（分）的函数图象是（ ）
| A． |  | B． |  | C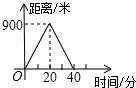． |  | D． |  |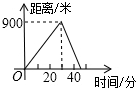
5．
有研究表明，长时间看手机会引发眼睛模糊、颈椎炎、记忆力下降等健康问题．某社区为了解居民平均每天看手机的时间t，随机抽取了社区内200人进行了抽查，调查数据统计如图表．
（1）平均每天看手机的时间不小于2小时的人数等于15人；
（2）如果按t各个范围的人数分布情况制作扇形统计图，那么表示平均每天看手机的时间小于0.5小时的扇形圆心角的度数n等于86.4°；
（3）若该社区共有居民1600人，估计平均每天看手机的时间小于1小时的人有多少？
有研究表明，长时间看手机会引发眼睛模糊、颈椎炎、记忆力下降等健康问题．某社区为了解居民平均每天看手机的时间t，随机抽取了社区内200人进行了抽查，调查数据统计如图表．（1）平均每天看手机的时间不小于2小时的人数等于15人；
（2）如果按t各个范围的人数分布情况制作扇形统计图，那么表示平均每天看手机的时间小于0.5小时的扇形圆心角的度数n等于86.4°；
（3）若该社区共有居民1600人，估计平均每天看手机的时间小于1小时的人有多少？
| 平均每天看手机的时间t（小时） | 人数（人） | 比例（%） |
| t＜0.5 | ||
| 0.5≤t＜1 | 38 | |
| 1≤t＜1.5 | 33% | |
| 1.5≤t＜2 | 33 | |
| t≥2 | 15 |
8．$\sqrt{\frac{1}{2}+\frac{1}{3}}$的值为（ ）
| A． | $\frac{1}{6}\sqrt{30}$ | B． | 6$\sqrt{30}$ | C． | $\frac{1}{6}\sqrt{5}$ | D． | 6$\sqrt{5}$ |
12．矩形ABCD中，两条对角线的长为6cm，且一夹角为60°，则矩形ABCD的周长为（ ）
| A． | 6+6$\sqrt{3}$ | B． | 6$\sqrt{3}$+6$\sqrt{2}$ | C． | 12 | D． | 18 |
如图是用程序计算函数值，若输入x的值为3，则输出的函数值y为$\frac{2}{3}$．