题目内容
20.已知一次函数y=kx-2k+1(k≠0),回答下列问题:(1)若此函数的图象过原点,求k的值;
(2)无论k取何值,该函数图象总经过一个定点,请你求出这个定点的坐标.
分析 (1)由一次函数图象经过原点,即可得出-2k+1=0,解之即可得出结论;
(2)由一次函数的解析式可得出(x-2)k=y-1,由“无论k取何值,该函数图象总经过一个定点”可得出x-2=0、y-1=0,解之即可得出该定点的坐标.
解答 解:(1)∵一次函数y=kx-2k+1的图象过原点,
∴-2k+1=0,
解得:k=$\frac{1}{2}$.
(2)∵y=kx-2k+1=k(x-2)+1,
∴(x-2)k=y-1.
∵无论k取何值,该函数图象总经过一个定点,即k有无数个解,
∴x-2=0,y-1=0,
解得:x=2,y=1.
∴这个定点的坐标(2,1).
点评 本题考查了一次函数图象上点的坐标特征,解题的关键是:(1)由一次函数图象经过原点,找出-2k+1=0;(2)将一次函数解析式变形为y=k(x-2)+1.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
11.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.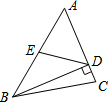 如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为( )
如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为( )
 如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为( )
如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为( )| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
12.已知直线y=kx+b经过点A(2,0),且与两坐标轴围成的直角三角形的面积为6,则k的值为( )
| A. | 3 | B. | -3 | C. | 3或-3 | D. | 6或-6 |
3.把m$\sqrt{-\frac{1}{m}}$化简后的结果为( )
| A. | $\sqrt{m}$ | B. | -m | C. | -$\sqrt{m}$ | D. | -$\sqrt{-m}$ |
 如图,将△ABC沿BC方向向右平移得到△DEF,其中BF=10,EC=4,则平移的距离为3.
如图,将△ABC沿BC方向向右平移得到△DEF,其中BF=10,EC=4,则平移的距离为3.