题目内容
如图，△ABC的一边AB为⊙O的直径，AC是⊙O的切线，且AB=AC，则∠C=考点：切线的性质
专题：
分析：根据切线的性质求出∠BAC=90°，根据等腰三角形性质得出∠C=∠B，根据三角形内角和定理求出即可．
解答：解：∵AC是⊙O的切线，
∴∠BAC=90°，
∵AB=AC，
∴∠C=∠B=45°，
故答案为：45°．
∴∠BAC=90°，
∵AB=AC，
∴∠C=∠B=45°，
故答案为：45°．
点评：本题考查了三角形内角和定理，切线的性质，等腰三角形的性质的应用，注意：圆的切线垂直于过切点的半径．
练习册系列答案
阅读快车系列答案
相关题目
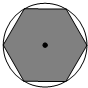如图，正六边形内接于⊙O，⊙O的直径为2分米，若在这个圆面上随意抛一粒豆子，则豆子落在正六边形内的概率是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
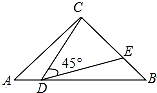如图，△ABC中，∠ACB=90°，AC=BC=2，点D在线段AB上运动（不包括端点），∠CDE=45°，DE与CB交于点E，若DB=x，CE=y．
如图：
如图，将一块直角三角形的直角顶点放在C（1，
如图，平面直角坐标系中，点A（2，9），B（2，3），C（3，2），D（9，2）在⊙P上，Q是⊙P上的一个动点．