题目内容
9.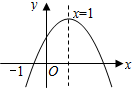 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②-b<a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②-b<a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 首先根据开口方向确定a的取值范围,根据对称轴的位置确定b的取值范围,根据抛物线与y轴的交点确定c的取值范围,根据抛物线与x轴是否有交点确定b2-4ac的取值范围,根据图象和x=2的函数值即可确定4a+2b+c的取值范围,根据x=1的函数值可以确定b<a+c是否成立.
解答 解:∵抛物线开口朝下,
∴a<0,
∵对称轴x=1=-$\frac{b}{2a}$,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
根据图象知道当x=-1时,y=a-b+c<0,
∴a+c<b,故②错误;
根据图象知道当x=2时,y=4a+2b+c>0,故③正确;
根据图象知道抛物线与x轴有两个交点,
∴b2-4ac>0,故④正确.
正确的有③④.
故选:B.
点评 此题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
19. 如图,已知△ABC与△DEF是全等三角形,则∠B=( )
如图,已知△ABC与△DEF是全等三角形,则∠B=( )
 如图,已知△ABC与△DEF是全等三角形,则∠B=( )
如图,已知△ABC与△DEF是全等三角形,则∠B=( )| A. | ∠F | B. | ∠D | C. | ∠DEF | D. | ∠A |
17.已知x=2是方程x2-mx+6=0的一个根,则m的值为( )
| A. | 5 | B. | -5 | C. | 6 | D. | -6 |
4.当x取x1、x2( x1≠x2)时,二次函数y=ax2+c的函数值相等,则当x取x1+x2时,函数值为( )
| A. | a+c | B. | a-c | C. | c | D. | -c |
18.方程-2x2+3=5x的根的情况是( )
| A. | 有两个相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个不相等的实数根 | D. | 只有一个实数根 |
 BD、CD分别是△ABC的两个外角∠CBE、∠BCF的平分线,求证:∠BDC=90°-$\frac{1}{2}$∠A.
BD、CD分别是△ABC的两个外角∠CBE、∠BCF的平分线,求证:∠BDC=90°-$\frac{1}{2}$∠A.