题目内容
7.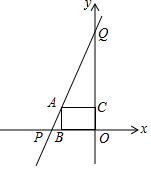 如图,直线y=2x+6与坐标轴分别交于P,Q两点,过函数图象上的点A分别作两坐标轴的垂线,垂足分别为B,C.
如图,直线y=2x+6与坐标轴分别交于P,Q两点,过函数图象上的点A分别作两坐标轴的垂线,垂足分别为B,C.(1)直接写出△OPQ的面积为9.
(2)点A的坐标可以用含有x的式子表示为(x,2x+6),若点A在线段PQ上,矩形ABOC的周长为8,求点A坐标;
(3)若点A在直线PQ上,以A、B、O、C为顶点的矩形周长为为16,直接写出所有符合条的点A坐标.
分析 (1)先根据直线y=2x+6与坐标轴分别交于P,Q两点,求得P(-3,0),Q(0,6),进而得出△OPQ的面积;
(2)根据点A在线段PQ上,点A的坐标为(x,2x+6),可得OB=-x,OC=2x+6,再根据矩形ABOC的周长为8,即可得出方程2(-x+2x+6)=8,进而得到点A坐标;
(3)分数轴情况进行讨论:①点A在第一象限时,x为正,2x+6为正,②点A在第二象限时,x为负,2x+6为正,③点A在第三象限时,x为负,2x+6为负,分别根据矩形周长为为16,列出方程进行求解即可.
解答 解:(1)∵直线y=2x+6与坐标轴分别交于P,Q两点,
∴P(-3,0),Q(0,6),
∴△OPQ的面积=$\frac{1}{2}$OP•OQ=$\frac{1}{2}$×3×6=9,
故答案为:9;
(2)∵点A在线段PQ上,点A的坐标为(x,2x+6),
∴OB=-x,OC=2x+6,
∵矩形ABOC的周长为8,
∴2(-x+2x+6)=8,
解得x=-2,
∴点A的坐标为(-2,2);
(3)∵点A在直线PQ上,
∴点A的位置分三种情况:
①点A在第一象限时,x为正,2x+6为正,
由题可得,16=2(x+2x+6),
解得x=$\frac{2}{3}$,
∴2x+6=$\frac{22}{3}$,
∴A($\frac{2}{3}$,$\frac{22}{3}$);
②点A在第二象限时,x为负,2x+6为正,
由题可得,16=2(-x+2x+6),
解得x=2(不合题意);
③点A在第三象限时,x为负,2x+6为负,
由题可得,16=2(-x-2x-6),
解得x=-$\frac{14}{3}$,
∴2x+6=-$\frac{10}{3}$,
∴A(-$\frac{14}{3}$,-$\frac{10}{3}$).
综上所述,点A的坐标为($\frac{2}{3}$,$\frac{22}{3}$)或(-$\frac{14}{3}$,-$\frac{10}{3}$).
点评 本题主要考查了矩形的性质以及一次函数图象上的点的坐标特征,解决问题的关键是依据直线经过的象限,进行分类讨论.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
| A. | (4030,1) | B. | (4029,-1) | C. | (4033,1) | D. | (4031,-1) |
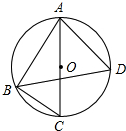 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )
如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )| A. | 95° | B. | 90° | C. | 85° | D. | 75° |
| A. | $\frac{1}{6}$ | B. | 6 | C. | -6 | D. | ±6 |

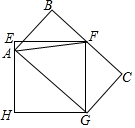 如图,正方形EFGH的边长为6厘米,长方形ABCG的长为8厘米,求CG的长.
如图,正方形EFGH的边长为6厘米,长方形ABCG的长为8厘米,求CG的长.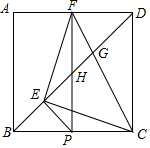 如图,正方形ABCD中,P为BC上一点,PE⊥BD于E,PF⊥AD于F,连接EF、CF.
如图,正方形ABCD中,P为BC上一点,PE⊥BD于E,PF⊥AD于F,连接EF、CF.
 画出函数y=$\frac{6}{x}$(x>0)的图象.
画出函数y=$\frac{6}{x}$(x>0)的图象.