题目内容
3.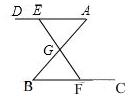 如图,在△ABC中,BC=4cm,过点A作射线AD∥BC,点E从点A出发沿射线AD以1cm/s的速度运动.同时点F从点B出发沿射线BC以1cm/s速度运动,连结EF交AB于点G,设点E运动时间为t(s).
如图,在△ABC中,BC=4cm,过点A作射线AD∥BC,点E从点A出发沿射线AD以1cm/s的速度运动.同时点F从点B出发沿射线BC以1cm/s速度运动,连结EF交AB于点G,设点E运动时间为t(s).(1)求证:AG=BG;
(2)求AE+CF的长(用含t的代数式表示);
(3)设△ABC的面积为a,直接写出当CF=2时△AEG的面积(用含a的代数式表示).
分析 (1)先判断出∠A=∠B,再有运动得出AE=BF,即可得出结论;
(2)先得出AE=BF,再分点F在线段BC和BC的延长线上,用线段的和差即可得出结论;
(3)先求出MG=$\frac{1}{4}$a,再分点F在线段BC和BC的延长线上,用线段的和差求出BF,即可求出AE,最后用三角形的面积公式即可得出结论.
解答 解:∵AD∥BC,
∴∠A=∠B,
由运动知,AE=t,BF=t,
∴AE=BF,
在△AEG和△BFG中,$\left\{\begin{array}{l}{∠AGE=∠BGF}\\{∠A=∠B}\\{AE=BF}\end{array}\right.$,
∴△AEG≌△BFG,
∴AG=BG;
(2)由(1)知,△AEG≌△BFG,
∴AE=BF,当点F在线段BC上时,AE+CF=BF+CF=BC=4cm;
当点F在线段BC的延长线上时,AE+CF=BF+CF=t+t-4=2t-4;
(3)如图,过点G作MN⊥BC,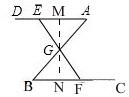
由(1)知,△AEG≌△BFG,
∴AE=BF,GM=GN=$\frac{1}{2}$MN.
∵S△ABC=$\frac{1}{2}$CB•MN=a,
∴MN=$\frac{2a}{BC}$=$\frac{1}{2}$a,
∴MG=$\frac{1}{4}$a,
当点F在线段BC上时,BF=BC-CF=4-2=2,
∴AE=2,
∴S△AEG=$\frac{1}{2}$AE•MG=$\frac{1}{2}$×2×$\frac{1}{4}$a=$\frac{1}{4}$a,
当点F在BC延长线上时,BF=BC+CF=4+2=6,
∴AE=6,
∴S△AEG=$\frac{1}{2}$AE•MG=$\frac{1}{2}$×6×$\frac{1}{4}$a=$\frac{3}{4}$a.
点评 此题是三角形综合题,主要考查了全等三角形的判定和性质,三角形的面积公式,还用到分类讨论的数学思想,解不同的关键是判断出AE=BF,是一道基础题目.

 阅读快车系列答案
阅读快车系列答案| A. | a<2 | B. | a>2 | C. | a<2,且a≠-4 | D. | a>2,且a≠4 |
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 客流量(万人次) | 8192 | 8371 | 8613 | 8994 | 9400 |
①若a:b=3:5,则a=3,b=5;
②比的前项和后项同时乘以或除以相同的数,比值不变;
③圆柱体积是圆锥体积的3倍;
④如果甲数比乙数多25%,那么乙数比甲数少20%.
其中正确的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
 如图,AD=BD,AE=EC,延长DE到F,使EF=DE,连接AF、FC、CD,求证:四边形DBCF是平行四边形.
如图,AD=BD,AE=EC,延长DE到F,使EF=DE,连接AF、FC、CD,求证:四边形DBCF是平行四边形.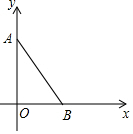 如图,平面直角坐标系xOy中,已知点A(0,3),点B($\sqrt{3}$,0),连接AB,若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
如图,平面直角坐标系xOy中,已知点A(0,3),点B($\sqrt{3}$,0),连接AB,若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.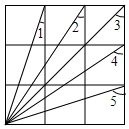 如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于225°.
如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于225°.