题目内容
如图，在
中，以
为直径的
交
于点
，点
为
的中点，连结
交于点
，且
.
（1）判断直线
与⊙O的位置关系，并证明你的结论；
（2）若的半径为2,
,求的长.
解：
⑴ 与⊙O相切
证明：连接
，
∵是的直径
∴
∴
∵
∴
又 ∵为的中点
∴
∴ 
即
又∵是直径
∴是的切线
（2）∵的半为2
∴
,
∵
由（1）知，
，
∴
,
∴
,
∵, 
∴
∽
，
∴
∴
，
设 
由勾股定理 
，
（舍负）
∴ 
练习册系列答案
相关题目
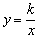的图象的一个交点为A(1 , m)．
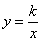的解析式；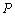
的坐标(不写求解过程)．
解：
B．
C
．
D．
有两个不相等的实数根，则实数k的取值范围 是 ．
的值是( ) 
D．6
与反比例函数
的图象相交于点A（－1，a），并且与x轴相交于点B． 