题目内容
18.如图,OC是∠AOM的平分线,OD是∠BOM的平分线.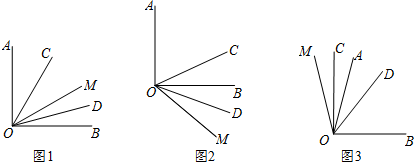
(1)如图1,若∠AOB=90°,∠AOM=60°,求∠COD的度数;
(2)如图2,若∠AOB=90°,∠AOM=130°,则∠COD=45°;
(3)如图3,若∠AOB=m°,∠AOM=n°,则∠COD=$\frac{1}{2}$m°.
分析 (1)直接利用角平分线的性质分别得出∠COM和∠DOM的值,进而得出答案;
(2)直接利用角平分线的性质分别得出∠COM和∠DOM的值,进而得出答案;
(3)直接利用角平分线的性质分别得出∠COM和∠DOM的值,进而得出答案.
解答 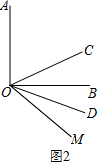
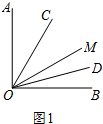 解:(1)如图1,∵∠AOB=90°,∠AOM=60°,
解:(1)如图1,∵∠AOB=90°,∠AOM=60°,
∴∠BOM=∠AOB-∠AOM=90°-60°=30°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=$\frac{1}{2}$∠AOM=$\frac{1}{2}$×60°=30°,
∠DOM=$\frac{1}{2}$∠BOM=$\frac{1}{2}$×30°=15°,
∴∠COD=∠COM+∠DOM=30°+15°=45°;
(2)如图2,∵∠AOB=90°,∠AOM=130°,
∴∠BOM=∠AOM-∠AOB=130°-90°=40°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=$\frac{1}{2}$∠AOM=$\frac{1}{2}$×130°=65°,
∠DOM=$\frac{1}{2}$∠BOM=$\frac{1}{2}$×40°=20°,
∴∠COD=∠COM-∠DOM=65°-20°=45°
故答案为:45. 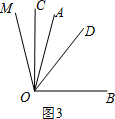
(3)如图3,∵∠AOB=m°,∠AOM=n°,
∴∠BOM=∠AOB+∠AOM=m°+n°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=$\frac{1}{2}$∠AOM=$\frac{1}{2}$×n°=$\frac{1}{2}$n°,
∠DOM=$\frac{1}{2}$∠BOM=$\frac{1}{2}$(m°+n°),
∴∠COD=∠DOM-∠COM=$\frac{1}{2}$(m°+n°)-$\frac{1}{2}$n°=$\frac{1}{2}$m°.
故答案为:$\frac{1}{2}$m.
点评 此题主要考查了角平分线的性质,正确掌握角平分线的性质是解题关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 8cm | B. | 16cm | C. | 8cm或16cm | D. | 15cm |
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 等边三角形 | D. | 等腰三角形 |