题目内容
10．
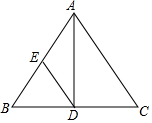已知：在△ABC中，AB=AC，AD⊥BC，垂足为D，点E是AB的中点，且AD=4，BC=6，则DE=$\frac{5}{2}$．
分析 先根据等腰三角形的性质得出BD的长，再由勾股定理求出AB的长，进而可得出结论．
解答 解：∵在△ABC中，AB=AC，AD⊥BC，BC=6，
∴BD=$\frac{1}{2}$BC=3．
∵AD=4，
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5．
∵点E是AB的中点，
∴DE=$\frac{1}{2}$AB=$\frac{5}{2}$．
故答案为：$\frac{5}{2}$．
点评 本题考查的是直角三角形斜边上的中线，熟知在直角三角形中，斜边上的中线等于斜边的一半是解答此题的关键．
练习册系列答案
能考试全能100分系列答案
相关题目
