题目内容
18．解不等式：$\frac{2x-1}{3}$-$\frac{5x+1}{2}$≥1，并把它的解集在数轴上表示出来．
分析 去分母，去括号，移项，合并同类项，相似化成1，即可求出不等式的解集．
解答 解：$\frac{2x-1}{3}$-$\frac{5x+1}{2}$≥1，
2（2x-1）-3（5x+1）≥6，
4x-2-15x-3≥6，
-11x≥11，
x≤-1，
在数轴上表示为
．
点评 本题考查了解一元一次不等式，在数轴上表示不等式组的解集的应用，能根据不等式的性质求出不等式的解集是解此题的关键．
练习册系列答案
相关题目
如图，在△ABC中，∠A=65°，若剪去∠A得到四边形BCDE，则∠1+∠2=245°．
如图，四边形ABCD中，AD∥BC，AB∥DC，AC与BD相交于O点，则图中一共有4对全等三角形．
13．填表：
| 2.5 | -$\sqrt{7}$ | $\root{3}{-8}$ | $\sqrt{17}$ | $\sqrt{3}$-1.7 | $\sqrt{3}-\frac{π}{2}$ | |
| 相反数 | -2.5 | $\sqrt{7}$ | $\root{3}{8}$ | -$\sqrt{17}$ | 1.7-$\sqrt{3}$ | $\frac{π}{2}$-$\sqrt{3}$ |
| 绝对值 | 2.5 | $\sqrt{7}$ | $\root{3}{8}$ | $\sqrt{17}$ | $\sqrt{3}$-1.7 | $\sqrt{3}$-$\frac{π}{2}$ |
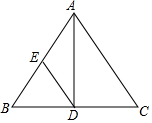已知：在△ABC中，AB=AC，AD⊥BC，垂足为D，点E是AB的中点，且AD=4，BC=6，则DE=$\frac{5}{2}$．