题目内容
15. ABC三地在同一条笔直的公路上,已知A地在B地与C地之间.甲车从A地出发先前往B地,再从B地前往C地与乙车会和;乙车与甲车同时出发,直接从B地前往C地,如图表示的是全过程中甲乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数关系.已知全过程中甲、乙两车速度均保持不变,乙车到达C地所用的时间是甲车到达B地所用时间的2倍,则甲车到达C地的时间为40小时.
ABC三地在同一条笔直的公路上,已知A地在B地与C地之间.甲车从A地出发先前往B地,再从B地前往C地与乙车会和;乙车与甲车同时出发,直接从B地前往C地,如图表示的是全过程中甲乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数关系.已知全过程中甲、乙两车速度均保持不变,乙车到达C地所用的时间是甲车到达B地所用时间的2倍,则甲车到达C地的时间为40小时.
分析 设甲车的速度为x千米/小时,乙车的速度为y千米/小时,根据速度×时间=路程即可得出关于x、y的二元一次方程组,解之即可得出甲、乙两车的速度,再根据路程=速度×时间即可求出B、C两地间的距离,利用时间=路程÷速度即可求出甲车到达C地的时间.
解答 解:设甲车的速度为x千米/小时,乙车的速度为y千米/小时,
根据题意得:$\left\{\begin{array}{l}{4(x+y)=400}\\{10x=400}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=40}\\{y=60}\end{array}\right.$,
∴B、C两地间的距离为60×10×2=1200(千米),
∴甲车到达C地的时间为(400+1200)÷40=40(小时).
故答案为:40.
点评 本题考查了函数的图象以及二元一次方程组的应用,根据速度×时间=路程列出关于x、y的二元一次方程组是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7. 如图,Rt△ABC中,∠BAC=90°,AB=$\sqrt{3}$,AC=1,在△ABC内依次作等边三角形,使一边在AB上,另一个顶点在BC边上,依次作出的等边三角形分别是第1个为△AA1B1,第2个为△B1A2B2,第3个△B2A3B3,…,则第2017个等边三角形的边长为( )
如图,Rt△ABC中,∠BAC=90°,AB=$\sqrt{3}$,AC=1,在△ABC内依次作等边三角形,使一边在AB上,另一个顶点在BC边上,依次作出的等边三角形分别是第1个为△AA1B1,第2个为△B1A2B2,第3个△B2A3B3,…,则第2017个等边三角形的边长为( )
 如图,Rt△ABC中,∠BAC=90°,AB=$\sqrt{3}$,AC=1,在△ABC内依次作等边三角形,使一边在AB上,另一个顶点在BC边上,依次作出的等边三角形分别是第1个为△AA1B1,第2个为△B1A2B2,第3个△B2A3B3,…,则第2017个等边三角形的边长为( )
如图,Rt△ABC中,∠BAC=90°,AB=$\sqrt{3}$,AC=1,在△ABC内依次作等边三角形,使一边在AB上,另一个顶点在BC边上,依次作出的等边三角形分别是第1个为△AA1B1,第2个为△B1A2B2,第3个△B2A3B3,…,则第2017个等边三角形的边长为( )| A. | $\frac{\sqrt{3}}{{2}^{2018}}$ | B. | $\frac{\sqrt{3}}{{2}^{2017}}$ | C. | $\frac{\sqrt{3}}{{2}^{2016}}$ | D. | $\frac{\sqrt{3}}{{2}^{2015}}$ |
4.一个等边三角形的边长为2,则这个三角形的面积是( )
| A. | 6 | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
2.计算(2x-1)2等于( )
| A. | 4x2+1 | B. | 4x2-2x+1 | C. | 4x2-4x-1 | D. | 4x2-4x+1 |

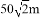 B.
B. 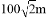 C.
C. 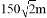 D.
D. 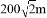

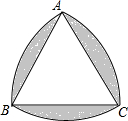 如图,三角形ABC是边长为2cm的等边三角形,分别以A,B,C三点为圆心,2cm为半径长画弧,那么阴影部分的周长为2πcm.(结果保留两位小数)
如图,三角形ABC是边长为2cm的等边三角形,分别以A,B,C三点为圆心,2cm为半径长画弧,那么阴影部分的周长为2πcm.(结果保留两位小数)