题目内容
4．一个等边三角形的边长为2，则这个三角形的面积是（ ）| A． | 6 | B． | 2 | C． | $\sqrt{5}$ | D． | $\sqrt{3}$ |
分析 根据等边三角形三线合一的性质可得D为BC的中点，即BD=CD，在直角三角形ABD中，已知AB、BD，根据勾股定理即可求得AD的长，即可求三角形ABC的面积，即可解题．
解答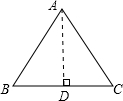 
解：∵等边三角形高线即中线，AB=2，
∴BD=CD=1，
在Rt△ABD中，AB=2，BD=1，
∴由勾股定理得，AD=$\sqrt{3}$，
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$，
故选：D．
点评 本题考查的是等边三角形的性质，熟知等腰三角形“三线合一”的性质是解题的关键．
练习册系列答案
相关题目
B. 
C. 
D. 
ABC三地在同一条笔直的公路上，已知A地在B地与C地之间．甲车从A地出发先前往B地，再从B地前往C地与乙车会和；乙车与甲车同时出发，直接从B地前往C地，如图表示的是全过程中甲乙两车之间的距离y（千米）与乙车行驶时间x（小时）之间的函数关系．已知全过程中甲、乙两车速度均保持不变，乙车到达C地所用的时间是甲车到达B地所用时间的2倍，则甲车到达C地的时间为40小时．
12．为鼓励居民节约用电，某市试行每户每月阶段电价加收费制，具体执行方案如表：
例如：一户居民七月份用电400度，则需缴电费200×0.55+100×0.65+100×0.85=260（元）．
（1）若小莹家六月份用电360度，则需缴电费多少元？
（2）已知小悦家五、六月份共用电540度，其中六月份用电量大于五月份用电量，共缴电费317元，问小悦家五、六月份各用电多少度？
| 每户每月用电数（度）阶段 | 阶段电价（元/度） |
| 小于等于200 | 0.55 |
| 大于200小于300的部分 | 0.65 |
| 大于等于300小于400的部分 | 0.8 |
| 大于等于400的部分 | 1 |
（1）若小莹家六月份用电360度，则需缴电费多少元？
（2）已知小悦家五、六月份共用电540度，其中六月份用电量大于五月份用电量，共缴电费317元，问小悦家五、六月份各用电多少度？
19．
从不同方向观察如图所示的几何体，不可能看到的是（ ）
从不同方向观察如图所示的几何体，不可能看到的是（ ）| A． |  | B． |  | C． |  | D． |  |
如图，AB=AD，BC=CD．求证：∠B=∠D．