题目内容
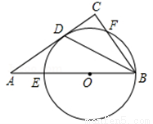
7. 如图,Rt△ABC中,∠BAC=90°,AB=$\sqrt{3}$,AC=1,在△ABC内依次作等边三角形,使一边在AB上,另一个顶点在BC边上,依次作出的等边三角形分别是第1个为△AA1B1,第2个为△B1A2B2,第3个△B2A3B3,…,则第2017个等边三角形的边长为( )
如图,Rt△ABC中,∠BAC=90°,AB=$\sqrt{3}$,AC=1,在△ABC内依次作等边三角形,使一边在AB上,另一个顶点在BC边上,依次作出的等边三角形分别是第1个为△AA1B1,第2个为△B1A2B2,第3个△B2A3B3,…,则第2017个等边三角形的边长为( )| A. | $\frac{\sqrt{3}}{{2}^{2018}}$ | B. | $\frac{\sqrt{3}}{{2}^{2017}}$ | C. | $\frac{\sqrt{3}}{{2}^{2016}}$ | D. | $\frac{\sqrt{3}}{{2}^{2015}}$ |
分析 根据题目已知条件可推出,AA1=$\frac{\sqrt{3}}{2}$AC=$\frac{\sqrt{3}}{2}$,B1A2=$\frac{1}{2}$A1B1=$\frac{\sqrt{3}}{{2}^{2}}$,依此类推,第n个等边三角形的边长等于$\frac{\sqrt{3}}{{2}^{n}}$,从而求解.
解答 解:∵AB=$\sqrt{3}$,AC=1,
∴BC=2,
∴∠ABC=30°,∠ACB=60°.
而△AA1B1为等边三角形,∠A1AB1=60°,
∴∠CAA1=30°,则∠CA1A=90°.
在Rt△CAA1中,AA1=$\frac{\sqrt{3}}{2}$AC=$\frac{\sqrt{3}}{2}$,
同理得:B1A2=$\frac{1}{2}$A1B1=$\frac{\sqrt{3}}{{2}^{2}}$,
依此类推,第n个等边三角形的边长等于$\frac{\sqrt{3}}{{2}^{n}}$,
则第2017个等边三角形的边长为$\frac{\sqrt{3}}{{2}^{2017}}$.
故选:B.
点评 本题主要考查勾股定理、等边三角形的性质及解直角三角形,关键是归纳出边长的规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知12与a的积为-48,则a比4小( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
12.为鼓励居民节约用电,某市试行每户每月阶段电价加收费制,具体执行方案如表:
例如:一户居民七月份用电400度,则需缴电费200×0.55+100×0.65+100×0.85=260(元).
(1)若小莹家六月份用电360度,则需缴电费多少元?
(2)已知小悦家五、六月份共用电540度,其中六月份用电量大于五月份用电量,共缴电费317元,问小悦家五、六月份各用电多少度?
| 每户每月用电数(度)阶段 | 阶段电价(元/度) |
| 小于等于200 | 0.55 |
| 大于200小于300的部分 | 0.65 |
| 大于等于300小于400的部分 | 0.8 |
| 大于等于400的部分 | 1 |
(1)若小莹家六月份用电360度,则需缴电费多少元?
(2)已知小悦家五、六月份共用电540度,其中六月份用电量大于五月份用电量,共缴电费317元,问小悦家五、六月份各用电多少度?
19. 从不同方向观察如图所示的几何体,不可能看到的是( )
从不同方向观察如图所示的几何体,不可能看到的是( )
 从不同方向观察如图所示的几何体,不可能看到的是( )
从不同方向观察如图所示的几何体,不可能看到的是( )| A. |  | B. |  | C. |  | D. |  |
14.阅读下列材料:
为了了解学校初二年级学生的阅读情况,小廉所在实践小组的同学们设计了相应的调查问卷,他们共发放问卷300张,收回有效问卷290张,并利用统计表整理了每一个问题的数据,绘制了统计图.他们的调查问卷中,有关“阅读载体的选择”和“阅读过书的类型”两个问题的统计情况如下表所示.
表1:
表2:
根据以上材料解答下列问题:
(1)根据表1中的统计数据,选择合适的统计图对其进行数据的描述;
(2)通过表2中统计出的数据你能得到哪些结论?请你说出其中的一条即可.
为了了解学校初二年级学生的阅读情况,小廉所在实践小组的同学们设计了相应的调查问卷,他们共发放问卷300张,收回有效问卷290张,并利用统计表整理了每一个问题的数据,绘制了统计图.他们的调查问卷中,有关“阅读载体的选择”和“阅读过书的类型”两个问题的统计情况如下表所示.
表1:
| 您的最主要阅读载体(限选一种) | ||||
| A.手机 | B.电脑 | C.电子书 | D.纸质书 | E.其他 |
| 45 | 30 | 75 | 130 | 10 |
| 您阅读过书的类型(可多选) | |||
| A.历史传记类 | B.社会哲学类 | C.科普科技类 | D.文学名著类 |
| 236 | 35 | 185 | 290 |
| E.报刊杂志类 | F.网络小说类 | G.漫画类 | H.其他160 |
| 216 | 85 | 196 | 160 |
(1)根据表1中的统计数据,选择合适的统计图对其进行数据的描述;
(2)通过表2中统计出的数据你能得到哪些结论?请你说出其中的一条即可.
 =0,则三角形的形状是( )
=0,则三角形的形状是( ) ABC三地在同一条笔直的公路上,已知A地在B地与C地之间.甲车从A地出发先前往B地,再从B地前往C地与乙车会和;乙车与甲车同时出发,直接从B地前往C地,如图表示的是全过程中甲乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数关系.已知全过程中甲、乙两车速度均保持不变,乙车到达C地所用的时间是甲车到达B地所用时间的2倍,则甲车到达C地的时间为40小时.
ABC三地在同一条笔直的公路上,已知A地在B地与C地之间.甲车从A地出发先前往B地,再从B地前往C地与乙车会和;乙车与甲车同时出发,直接从B地前往C地,如图表示的是全过程中甲乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数关系.已知全过程中甲、乙两车速度均保持不变,乙车到达C地所用的时间是甲车到达B地所用时间的2倍,则甲车到达C地的时间为40小时. 如图,AB=AD,BC=CD.求证:∠B=∠D.
如图,AB=AD,BC=CD.求证:∠B=∠D.