题目内容
5. 如图,菱形ABCD的周长为16,面积为12,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于3.
如图,菱形ABCD的周长为16,面积为12,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于3.
分析 连结AP,由菱形ABCD的周长为16,根据了菱形的性质得AB=AD=4,并且S菱形ABCD=2S△ABD,则S△ABD=$\frac{1}{2}$×12=6,由于S△ABD=S△APB+S△APD,再根据三角形的面积公式得到$\frac{1}{2}$•PE•AB+$\frac{1}{2}$•PF•AD=6,即可得到PE+PF的值.
解答 解:连结AP,如图,
∵菱形ABCD的周长为16,
∴AB=AD=4,
∴S菱形ABCD=2S△ABD,
∴S△ABD=$\frac{1}{2}$×12=6,
而S△ABD=S△APB+S△APD,PE⊥AB,PF⊥AD,
∴$\frac{1}{2}$•PE•AB+$\frac{1}{2}$•PF•AD=6,
∴2PE+2PF=6,
∴PE+PF=3,
故答案为:3.
点评 本题主要考查了菱形的性质:菱形的对边分别平行,四条边都相等,两条对角线互相垂直平分,并且分别平分两组内角,也考查了三角形的面积公式,作出适当的辅助线,利用三角形的面积和菱形的面积建立等量关系是解答此题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
20.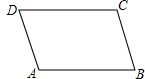 已知:如图,平行四边形ABCD,求作一个三角形,使三角形的面积等于平行四边形ABCD的面积.甲、乙两人的作法分别是:
已知:如图,平行四边形ABCD,求作一个三角形,使三角形的面积等于平行四边形ABCD的面积.甲、乙两人的作法分别是:
甲:
1.过C作AB的垂线段CE,垂足为E;
2.延长EC到点F,使得CE=CF;
3.连结AF、BF;△ABF即为所求的三角形
乙:
1.连结AC和BD,相交于点O;
2.延长OC到点E,使得OE=AC;
3.延长OB到点F,使得OF=DB;
4.连结EF;△OEF即为所求的三角形
对于甲、乙两人的作法,可判断( )
 已知:如图,平行四边形ABCD,求作一个三角形,使三角形的面积等于平行四边形ABCD的面积.甲、乙两人的作法分别是:
已知:如图,平行四边形ABCD,求作一个三角形,使三角形的面积等于平行四边形ABCD的面积.甲、乙两人的作法分别是:甲:
1.过C作AB的垂线段CE,垂足为E;
2.延长EC到点F,使得CE=CF;
3.连结AF、BF;△ABF即为所求的三角形
乙:
1.连结AC和BD,相交于点O;
2.延长OC到点E,使得OE=AC;
3.延长OB到点F,使得OF=DB;
4.连结EF;△OEF即为所求的三角形
对于甲、乙两人的作法,可判断( )
| A. | 甲、乙均正确 | B. | 甲、乙均错 | C. | 甲正确、乙错误 | D. | 甲错误,乙正确 |
17.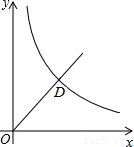 如图,在平面直角坐标系中,函数y=x和函数y=$\frac{16}{x}$的图象在第一象限交于点D(4,m),与平行于y轴的直线x=t(0<t<4)分别交于点A和点B,平面上有点P(0,6).若以点O,P,A,B为顶点的四边形为平行四边形,则这个平行四边形被直线PD所分割成的两部分图形的面积之比为( )
如图,在平面直角坐标系中,函数y=x和函数y=$\frac{16}{x}$的图象在第一象限交于点D(4,m),与平行于y轴的直线x=t(0<t<4)分别交于点A和点B,平面上有点P(0,6).若以点O,P,A,B为顶点的四边形为平行四边形,则这个平行四边形被直线PD所分割成的两部分图形的面积之比为( )
 如图,在平面直角坐标系中,函数y=x和函数y=$\frac{16}{x}$的图象在第一象限交于点D(4,m),与平行于y轴的直线x=t(0<t<4)分别交于点A和点B,平面上有点P(0,6).若以点O,P,A,B为顶点的四边形为平行四边形,则这个平行四边形被直线PD所分割成的两部分图形的面积之比为( )
如图,在平面直角坐标系中,函数y=x和函数y=$\frac{16}{x}$的图象在第一象限交于点D(4,m),与平行于y轴的直线x=t(0<t<4)分别交于点A和点B,平面上有点P(0,6).若以点O,P,A,B为顶点的四边形为平行四边形,则这个平行四边形被直线PD所分割成的两部分图形的面积之比为( )| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 1:4 |
14.某厂生产纪念章10万个,质检科为检测这批纪念章质量的合格情况从中随机抽查500个,合格498个,下列说法正确的是( )
| A. | 总体是10万个纪念章,样本是500个纪念章 | |
| B. | 总体是10万个纪念章,样本是498个纪念章 | |
| C. | 总体是500万个纪念章,样本是500个纪念章 | |
| D. | 总体是10万个纪念章,样本是2个纪念章 |
15. 如图,在边长为1的正方形构成的网络中,半径为1的⊙O的圆心在格点上,则图中阴影部分两个小扇形的面积之和为( )
如图,在边长为1的正方形构成的网络中,半径为1的⊙O的圆心在格点上,则图中阴影部分两个小扇形的面积之和为( )
 如图,在边长为1的正方形构成的网络中,半径为1的⊙O的圆心在格点上,则图中阴影部分两个小扇形的面积之和为( )
如图,在边长为1的正方形构成的网络中,半径为1的⊙O的圆心在格点上,则图中阴影部分两个小扇形的面积之和为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{6}$ |
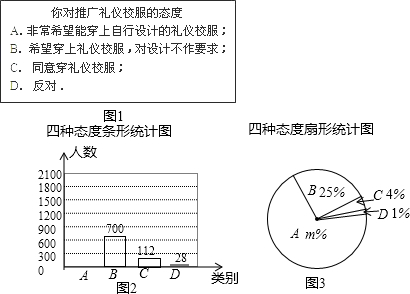
 如图,四边形ABCD为菱形,点D、C落在以B为圆心的弧EF上,则∠A的度数为60°.
如图,四边形ABCD为菱形,点D、C落在以B为圆心的弧EF上,则∠A的度数为60°.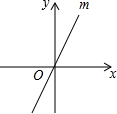 如图,在平面直角坐标系中,直线m经过原点,且与x轴正半轴成60度的角.若点N到x轴、直线m的距离分别为2和1,则点N的坐标为(0,2)或(0,-2)或($\frac{4\sqrt{3}}{3}$,2)或(-$\frac{4\sqrt{3}}{3}$,-2).
如图,在平面直角坐标系中,直线m经过原点,且与x轴正半轴成60度的角.若点N到x轴、直线m的距离分别为2和1,则点N的坐标为(0,2)或(0,-2)或($\frac{4\sqrt{3}}{3}$,2)或(-$\frac{4\sqrt{3}}{3}$,-2).