题目内容
4. 嘉淇想证明三角形内角和是180°和其他一些的命题.请完成下列一些命题和证明.
嘉淇想证明三角形内角和是180°和其他一些的命题.请完成下列一些命题和证明.(1)怎样证明三角形内角和是180°呢?
(2)已知命题:等腰三角形底边上的中线和顶角的角平分线重合,证明这个命题,并写出它的逆命题,逆命题成立吗?
命题:底边上的中线和顶角的角平分线重合的三角形是等腰三角形
证明:证明:在△ABD和△ACD中,
∵$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD
由此我们不难发现:此命题是互逆命题
那么怎样证明呢?请写出证明过程.(可以画出作图痕迹.)
分析 (1)先写出已知、证明,过点C作CD∥AB,点E为BC的延长线上一点,利用平行线的性质得到∠1=∠A,∠2=∠B,然后根据平角的定义进行证明;
(2)根据证明的步骤,先写出已知、求证,再写出证明过程,最后写出逆命题即可.
解答  解:(1)已知:△ABC,如图1,
解:(1)已知:△ABC,如图1,
求证:∠A+∠B+∠C=180°,
证明:过点C作CD∥AB,点E为BC的延长线上一点,如图,
∵CD∥AB,
∴∠1=∠A,∠2=∠B,
∵∠C+∠1+∠2=180°,
∴∠A+∠B+∠C=180°.
(2)如图2,已知:△ABC中,AB=AC,AD是BC边的中线,
求证:∠BAD=∠CAD.
证明:在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD.
它的逆命题是:底边上的中线和顶角的角平分线重合的三角形是等腰三角形,成立.
点评 本题考查了三角形内角和定理:三角形内角和是180°.本题的关键时把三角形三个角的和转化为一个平角,同时注意文字题证明的步骤书写.

练习册系列答案
相关题目
12.计算:
(1)计算:($\sqrt{2}$+π)0-|-3|+($\frac{1}{2}$)-1
(2)化简:(1-$\frac{1}{x-1}$)÷$\frac{x-2}{{x}^{2}-1}$.
(1)计算:($\sqrt{2}$+π)0-|-3|+($\frac{1}{2}$)-1
(2)化简:(1-$\frac{1}{x-1}$)÷$\frac{x-2}{{x}^{2}-1}$.
9.抛三枚硬币,两个正面和一个反面朝上的概率是( )
| A. | $\frac{7}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{8}$ |
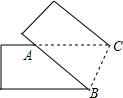 将一张宽为4cm的矩形纸片折叠成如图所示图形,若AB=6cm,则AC的长度为6cm.
将一张宽为4cm的矩形纸片折叠成如图所示图形,若AB=6cm,则AC的长度为6cm. 如图是由6个相同的小立方块搭成的几何体,那么这个几何体的左视图是( )
如图是由6个相同的小立方块搭成的几何体,那么这个几何体的左视图是( )


