题目内容

9．下列三组正多边形的组合：①正八边形和正方形；②正五边形和正八边形；③正六边形和正方形，能够铺满地面的组合是①（填序号即可）

分析 能够铺满地面的图形，即是能够凑成360°的图形组合．

解答 解：①正方形的每个内角为90°，正八边形的每个内角为135°，两个正八边形和一个正方形刚好能铺满地面；
②正五边形每个内角是180°-360°÷5=108°，正八边形每个内角为135度，135m+108n=360°，显然n取任何正整数时，m不能得正整数，故不能铺满；
③正六边形的每个内角是120°，正方形的每个内角是90°，120m+90n=360°，显然n取任何正整数时，m不能得正整数，故不能铺满；
故答案为：①．

点评 此题主要考查了平面镶嵌，解这类题，除了掌握多边形镶嵌成平面图形的条件，还可列二元方程看是否有正整数解来判断．

练习册系列答案
相关题目
19．已知正方形OABC的边OC、OA分别在x、y轴的正半轴上，点B坐标为（10，10），点P从O出发沿O→C→B运动，速度为1个单位每秒，连接AP．设运动时间为t．
（1）若抛物线y=-（x-h）2+k经过A、B两点，求抛物线函数关系式；
（2）当0≤t≤10时，如图1，过点O作OH⊥AP于点H，直线OH交边BC于点D，连接AD，PD，设△APD的面积为S，求S的最小值；
（3）在图2中以A为圆心，OA长为半径作⊙A，当0≤t≤20时，过点P作PQ⊥x轴（Q在P的上方），且线段PQ=t+12：
①当t在什么范围内，线段PQ与⊙A只有一个公共点？当t在什么范围内，线段PQ与⊙A有两个公共点？
②请将①中求得的t的范围作为条件，证明：当t取该范围内任何值时，线段PQ与⊙A总有两个公共点．
20．在正方形ABCD中，AB=2，．
（1）如图1，点P是对角线AC上任一点，若M是AB中点，求PM+PB的最小值；
（2）如图2，点P是对角线AC上任一点，若M，N分别是边AB，BC上的点，且AM=$\frac{1}{2}$AB，CN=$\frac{1}{3}$BC，求PM+PN的最小值．
（3）如图3，若M1，M2是AB边三等分点，P1，P2是对角线AC上任意两点，求（P1B+P1M1）2+（P2M1+P2M2）2的最小值．
17．计算
（1）解方程组$\left\{\begin{array}{l}{x-y=13}\\{x=6y-7}\end{array}\right.$
（2）解不等式组$\left\{\begin{array}{l}{5x-9＜3（x-1）}\\{1-\frac{3}{2}x≤\frac{1}{2}x-1}\end{array}\right.$．
4．若关于x的不等式组$\left\{\begin{array}{l}{x-a＞0}\\{1-2x＞x-2}\end{array}\right.$的解集中只有4个整数解，则a取值范围是-4≤a＜-3．
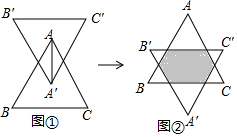14．如图①，等边三角形ABC和等边三角形A′B′C′的边长均为2，且BC∥B′C′，将等边三角形ABC沿A′A方向向上平移到图②的位置，则阴影部分的周长为4．
1．数据1，1，1，3，4的平均数是2，众数是1，中位数是1．
18．要使$\frac{1}{\sqrt{x-2}}$有意义，x必须满足（　　）
A．x≤2B．x＞2C．x≥2D．x＜2
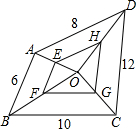19．如图，点O为四边形ABCD内任意一点，E，F，G，H分别为边OA，OB，OC，OD的中点，则四边形EFGH的周长=18．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网