��Ŀ����
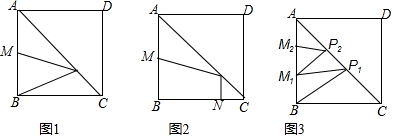
20����������ABCD�У�AB=2������1����ͼ1����P�ǶԽ���AC����һ�㣬��M��AB�е㣬��PM+PB����Сֵ��
��2����ͼ2����P�ǶԽ���AC����һ�㣬��M��N�ֱ��DZ�AB��BC�ϵĵ㣬��AM=$\frac{1}{2}$AB��CN=$\frac{1}{3}$BC����PM+PN����Сֵ��
��3����ͼ3����M1��M2��AB�����ȷֵ㣬P1��P2�ǶԽ���AC���������㣬��P1B+P1M1��2+��P2M1+P2M2��2����Сֵ��
���� ��1����ͼ1�У�����PD��DM��B��D����AC�Գƣ��Ƴ�PB=PD���Ƴ�PB+PM=PD+PM���ڡ�PDM�У���֪PD+PM��DM�����DM���ɽ�����⣻
��2����ͼ2�У�ȡAD���е�F������PF��FN����NH��AD��H����ΪM��F����AC�Գƣ��Ƴ�PM=PF���ɵ�PM+PN=PF+PN���ڡ�PFN�У�PF+PN��FN���ɴ����FN���ɽ�����⣻
��3���ֱ����P1B+P1M1��P2M1+P2M2����Сֵ���ɽ�����⣻
��� �⣺��1����ͼ1�У�����PD��DM��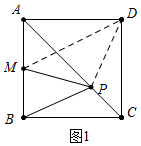
���ı���ABCD�������Σ�
��AB=CB=CD=AD=2����BAD=90�㣬
��Rt��ADM��DM=$\sqrt{A{D}^{2}+A{M}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$��
��B��D����AC�Գƣ�
��PB=PD��
��PB+PM=PD+PM��
�ڡ�PDM�У���֪PD+PM��DM��
��PM+PB��$\sqrt{5}$��
��PM+PB����СֵΪ$\sqrt{5}$��
��2����ͼ2�У�ȡAD���е�F������PF��FN����NH��AD��H��
��֪�ı���NHDC�Ǿ��Σ�
��CN=DH=$\frac{2}{3}$��DF=1��
��FH=DF-DH=1-$\frac{2}{3}$=$\frac{1}{3}$��
��Rt��FNH��FN=$\sqrt{N{H}^{2}+F{H}^{2}}$=$\frac{\sqrt{37}}{3}$��
��AM=BM��AF=FD��
��M��F����AC�Գƣ�
��PM=PF��
��PM+PN=PF+PN��
�ڡ�PFN�У�PF+PN��FN��
��PM+PN��$\frac{\sqrt{37}}{3}$��
��PM+PN����СֵΪ$\frac{\sqrt{37}}{3}$��
��3����ͼ3�У���AD��ȡһ��N��ʹ��AN=AM2������NM1��NP2��DM1��DP1��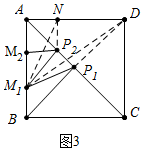
��Rt��ANM1��NM1=$\sqrt{A{N}^{2}+A{{M}_{1}}^{2}}$=$\frac{2\sqrt{5}}{3}$��
��Rt��ADM1��DM1=$\sqrt{A{D}^{2}+A{{M}_{1}}^{2}}$=$\frac{2\sqrt{13}}{3}$��
��N��M2����AC�Գƣ�
��P2N=P2M2��
��P2M+P2M1=P2N+P2M1��NM1��
��P2M+P2M1����СֵΪ$\frac{2\sqrt{5}}{3}$��
ͬ����P1B+P1M1�TP1D+P1M1��DM1��
��P1B+P1M1����СֵΪ$\frac{2\sqrt{13}}{3}$��
�ࣨP1B+P1M1��2+��P2M1+P2M2��2����Сֵ=$\frac{20}{9}$+$\frac{52}{9}$=8��
���� ���⿼�������ε����ʡ�����֮���߶���̡����ɶ�������ԳƵ�֪ʶ������Ĺؼ������������Գƽ����ֵ���⣬�����п��������ͣ�

| A�� | ������������ǡ���п��� | B�� | ͬλ����� | ||
| C�� | ���ֻ�����δ�ӵ绰 | D�� | �������ڽǺ͵���180�� |
| A�� | x2+3x2=4x4 | B�� | x2y•2x3=2x6y | C�� | ��6x3y2���£�3x��=2x2 | D�� | ��-3x��2=9x2 |
 ��ͼ��ʾ����֪��A=��F����C=��D����ͼ��գ�����������ע�����ɣ�
��ͼ��ʾ����֪��A=��F����C=��D����ͼ��գ�����������ע�����ɣ�