题目内容
3.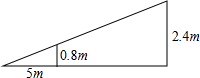 如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )
如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )| A. | 15米处 | B. | 10米处 | C. | 8米处 | D. | 7.5米处 |
分析 根据题意得出:△AFD∽△ABC,进而利用相似三角形的性质得出即可.
解答  解:如图所示:由题意可得,△AFD∽△ABC,
解:如图所示:由题意可得,△AFD∽△ABC,
则$\frac{AF}{AB}$=$\frac{DF}{BC}$,
即$\frac{5}{5+BF}$=$\frac{0.8}{2.4}$,
解得:BF=10,
则她的击球高度是2.4米,则应站在离网的10米处.
故选:B.
点评 此题主要考查了相似三角形的应用,利用相似三角形的性质得出是解题关键.

练习册系列答案
相关题目
18.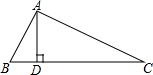 如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )
如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )
 如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )
如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 2 | D. | 3 |
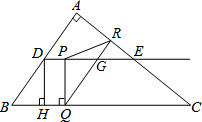 如图,在Rt△ABC中,∠A=90°,AB=6cm,AC=8cm,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向以1cm/s的速度运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,交DE于G,当点Q与点C重合时,点P停止运动.设点P运动时间为ts.
如图,在Rt△ABC中,∠A=90°,AB=6cm,AC=8cm,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向以1cm/s的速度运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,交DE于G,当点Q与点C重合时,点P停止运动.设点P运动时间为ts. 在平面直角坐标系xOy中,抛物线y=-$\frac{1}{2}$(x+m)2的顶点为A,直线y=-x-m与y轴相交于点B,其中m>0.
在平面直角坐标系xOy中,抛物线y=-$\frac{1}{2}$(x+m)2的顶点为A,直线y=-x-m与y轴相交于点B,其中m>0. 如图,在边长为1的正方形纸板上,依次贴上面积为$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$的长方形彩色纸片(n为大于1的整数),请你用“数形结合”的思想,依数形变化的规律,计算
如图,在边长为1的正方形纸板上,依次贴上面积为$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$的长方形彩色纸片(n为大于1的整数),请你用“数形结合”的思想,依数形变化的规律,计算