题目内容
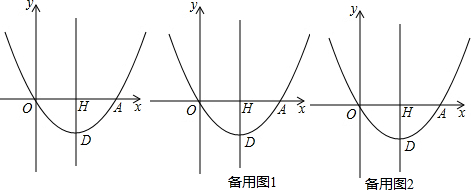
8. 在平面直角坐标系xOy中,抛物线y=-$\frac{1}{2}$(x+m)2的顶点为A,直线y=-x-m与y轴相交于点B,其中m>0.
在平面直角坐标系xOy中,抛物线y=-$\frac{1}{2}$(x+m)2的顶点为A,直线y=-x-m与y轴相交于点B,其中m>0.(1)判断点A是否在直线y=-x-m上;
(2)点C是抛物线对称轴上的一点,点D在抛物线上,若以C、D、A为顶点的三角形与△AOB全等,求出m的值和点D的坐标.
分析 (1)根据顶点式得出点A的坐标代入解答即可;
(2)根据等腰直角三角形的性质得出∠DAC=45°,AD=AB或AD=AO两种情况进行解答.
解答 解:(1)因为抛物线y=-$\frac{1}{2}$(x+m)2的顶点为A,
可得点A的坐标为:(-m,0),
把A(-m,0)代入y=-x-m中,
可得:0=-(-m)-m成立,
∴A在直线上;
(2)因为直线y=-x-m与y轴相交于点B,可得点B的坐标为(0,-m),
所以△AOB是等腰直角三角形,
若△CDA与△AOB全等,
∵∠DAC≠90°,
∴必有∠DAC=45°,且AD=AB或AD=AO,
①若∠DAC=45°,AD=AB=$\sqrt{2}$m,
则D(0,-m)或D(-2m,-m)代入y=-$\frac{1}{2}$(x+m)2,
得:m=0或2,
∵m>0,
∴m=2,
点D坐标为(0,-2)或(-4,-2);
②若∠DAC=45°,AD=AO=m,
则D($-m±\frac{\sqrt{2}}{2}m$,-$\frac{\sqrt{2}}{2}m$)代入y=-$\frac{1}{2}$(x+m)2,
得:m=0或2$\sqrt{2}$,
∵m>0,
∴m=2$\sqrt{2}$,
点D的坐标为($-2\sqrt{2}±2$,-2).
点评 此题考查一次函数综合题,关键是根据顶点式得出点A的坐标,再根据等腰直角三角形的性质进行解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.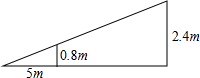 如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )
如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )
 如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )
如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )| A. | 15米处 | B. | 10米处 | C. | 8米处 | D. | 7.5米处 |