题目内容
13. 如图,在边长为1的正方形纸板上,依次贴上面积为$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$的长方形彩色纸片(n为大于1的整数),请你用“数形结合”的思想,依数形变化的规律,计算
如图,在边长为1的正方形纸板上,依次贴上面积为$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$的长方形彩色纸片(n为大于1的整数),请你用“数形结合”的思想,依数形变化的规律,计算1-($\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$)=$\frac{1}{{2}^{n}}$.
分析 如果假设图中阴影的部分就是面积为$\frac{1}{{2}^{n}}$的彩色纸片,那么所求的式子其实就是正方形纸板上被彩色纸片所覆盖的面积.那么没有被彩色纸片所覆盖的面积为多少呢根据题目可以很容易的看出,没有被彩色纸片覆盖的面积为$\frac{1}{{2}^{n-1}}$-$\frac{1}{{2}^{n}}$=$\frac{1}{{2}^{n}}$.
解答 解:∵$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$,
∴1-($\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$)=$\frac{1}{{2}^{n}}$,
故答案为:$\frac{1}{{2}^{n}}$.
点评 本题主要考查了图形的变化规律,发现规律是解答此题的关键.

练习册系列答案
相关题目
3.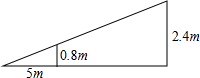 如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )
如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )
 如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )
如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )| A. | 15米处 | B. | 10米处 | C. | 8米处 | D. | 7.5米处 |
4.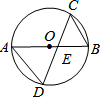 如图,AB是⊙O的直径,它与弦CD交于点E.我们给出下列结论:
如图,AB是⊙O的直径,它与弦CD交于点E.我们给出下列结论:
①AE•BE=CE•DE;②△ADE∽△CBE;③∠A=∠C;④∠AED=∠BEC
这些结论中正确的是( )
 如图,AB是⊙O的直径,它与弦CD交于点E.我们给出下列结论:
如图,AB是⊙O的直径,它与弦CD交于点E.我们给出下列结论:①AE•BE=CE•DE;②△ADE∽△CBE;③∠A=∠C;④∠AED=∠BEC
这些结论中正确的是( )
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ②③④ |
5.已知|x|=3,|y|=2,且xy<0,则x-y的值等于( )
| A. | -1或1 | B. | 5或-5 | C. | 5或-1 | D. | -5或1 |
 如图,矩形ABCD中,AB=6,AD=8,P是BC上的点,PE⊥BD于E,PF⊥AC于F,则PF+PE=$\frac{24}{5}$.
如图,矩形ABCD中,AB=6,AD=8,P是BC上的点,PE⊥BD于E,PF⊥AC于F,则PF+PE=$\frac{24}{5}$.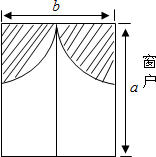 小明房间窗户的装饰物如图所示,它们由两个四分之一圆组成:
小明房间窗户的装饰物如图所示,它们由两个四分之一圆组成: