题目内容
 如图,BO、CO分别平分∠ABC和∠ACB.
如图,BO、CO分别平分∠ABC和∠ACB.(1)若∠A=70°,求∠BOC的度数;
(2)直接写出∠BOC与∠A的关系.
考点:三角形内角和定理
专题:
分析:(1)根据三角形的内角和定理求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,然后根据三角形的内角和等于180°列式计算即可得解;
(2)由(1)直接得出答案即可.
(2)由(1)直接得出答案即可.
解答:解:(1)∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=180°-70°=110°,
∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×110°=55°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
(2)∠BOC=180°-(∠OBC+∠OCB)
=180°-
(∠ABC+∠ACB)
=180°-
(180°-∠A)
=90°+
∠A.
∴∠ABC+∠ACB=180°-∠A=180°-70°=110°,
∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
(2)∠BOC=180°-(∠OBC+∠OCB)
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
相关题目
 如图,由六个全等的正三角形拼成的图,图中平行四边形的个数是( )
如图,由六个全等的正三角形拼成的图,图中平行四边形的个数是( )| A、4个 | B、6个 | C、8个 | D、10个 |
在数轴上表示不等式-x≤2的解集,正确的是( )
A、 |
B、 |
C、 |
D、 |
小明家承包的果园,前年水果产量为50吨,后来改进了种植技术,今年的总产量是60.5吨,小明家去年,今年平均每年的粮食产量增长率是( )
| A、5% | B、10% |
| C、15% | D、20% |
 已知m,n是方程l的两个实数根,且m<n.如图,若抛物线l的图象经过点A(m,0),B(0,n).
已知m,n是方程l的两个实数根,且m<n.如图,若抛物线l的图象经过点A(m,0),B(0,n). 如图,AB是⊙O的直径,BC是弦,∠ABC的平分线BD交⊙O于点D,DE⊥BC,交BC的延长线于点E,BD交AC于点F.
如图,AB是⊙O的直径,BC是弦,∠ABC的平分线BD交⊙O于点D,DE⊥BC,交BC的延长线于点E,BD交AC于点F.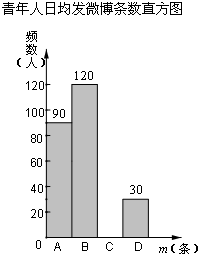 在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:青年人日均发微博条数统计表
在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:青年人日均发微博条数统计表
 如图,六边形ABCDEF的内角都相等,∠DAB=60°.AB与DE有什么关系?为什么?
如图,六边形ABCDEF的内角都相等,∠DAB=60°.AB与DE有什么关系?为什么?