题目内容
 已知m,n是方程l的两个实数根,且m<n.如图,若抛物线l的图象经过点A(m,0),B(0,n).
已知m,n是方程l的两个实数根,且m<n.如图,若抛物线l的图象经过点A(m,0),B(0,n).(1)求抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为C,抛物线的顶点为D,求C,D的坐标和△BCD的面积;
(3)已知P是线段OC上一点,过点P作PH⊥x轴,交抛物线于点H,若直线BC把△PCH分成面积相等的两部分,求P点的坐标.
考点:二次函数综合题
专题:
分析:(1)首先解方程求得A、B两点的坐标,然后利用待定系数法确定二次函数的解析式即可;
(2)根据解方程直接写出点C的坐标,然后确定顶点的坐标,过D作DE⊥x轴于E,利用S△BCD=S△CDE+S梯形OBDE-S△OBC求解即可;
(3)设P(a,0),则H(a,-a2-4a+5),由于直线BC把△PCH分成面积相等的两部分,须且只须BC等分线段PH,亦即PH的中点(a,
)在直线BC上.代入BC的解析式y=x+5即可求得a的值,从而写出点C的坐标.
(2)根据解方程直接写出点C的坐标,然后确定顶点的坐标,过D作DE⊥x轴于E,利用S△BCD=S△CDE+S梯形OBDE-S△OBC求解即可;
(3)设P(a,0),则H(a,-a2-4a+5),由于直线BC把△PCH分成面积相等的两部分,须且只须BC等分线段PH,亦即PH的中点(a,
| -a2-4a+5 |
| 2 |
解答:解:(1)由方程x2-6x+5=0得x1=1,x2=5,
∵m<n,
∴m=1,n=5,
∴A(1,0),B(0,5).
把A(1,0),B(0,5)代入y=-x2+bx+c得:
,
解得
,
∴抛物线的解析式y=-x2-4x+5;
(2)C(-5,0),D(-2,9),
过D作DE⊥x轴于E,
∵易得E(-2,0).
∴S△BCD=S△CDE+S梯形OBDE-S△OBC=
×3×9+
×2-
×5×5=15;
(3)设P(a,0),则H(a,-a2-4a+5),由于直线BC把△PCH分成面积相等的两部分,
须且只须BC等分线段PH,亦即PH的中点(a,
)在直线BC上.
∵易得直线BC的解析式为y=x+5,
∴
=a+5,
解得a1=-1,a2=-5(不合题意,舍去),
∴P点坐标为(-1,0).
∵m<n,
∴m=1,n=5,
∴A(1,0),B(0,5).
把A(1,0),B(0,5)代入y=-x2+bx+c得:
|
解得
|
∴抛物线的解析式y=-x2-4x+5;
(2)C(-5,0),D(-2,9),
过D作DE⊥x轴于E,
∵易得E(-2,0).
∴S△BCD=S△CDE+S梯形OBDE-S△OBC=
| 1 |
| 2 |
| 5+9 |
| 2 |
| 1 |
| 2 |
(3)设P(a,0),则H(a,-a2-4a+5),由于直线BC把△PCH分成面积相等的两部分,
须且只须BC等分线段PH,亦即PH的中点(a,
| -a2-4a+5 |
| 2 |
∵易得直线BC的解析式为y=x+5,
∴
| -a2-4a+5 |
| 2 |
解得a1=-1,a2=-5(不合题意,舍去),
∴P点坐标为(-1,0).
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
下列说法不正确的是( )
| A、-1的立方根是-1 |
| B、-1的平方根是-1 |
| C、-1的平方是1 |
| D、1的平方根是±1 |
 如图,点A(2,6)和点B(点B在点A的右侧)在反比例函数的图象上,点C在y轴上,BC∥x轴,tan∠ACB=2,二次函数的图象经过A、B、C三点.
如图,点A(2,6)和点B(点B在点A的右侧)在反比例函数的图象上,点C在y轴上,BC∥x轴,tan∠ACB=2,二次函数的图象经过A、B、C三点. 如图,BO、CO分别平分∠ABC和∠ACB.
如图,BO、CO分别平分∠ABC和∠ACB.
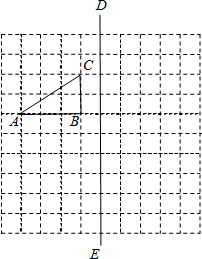 在所给的正方形网格中,每个小正方形的边长均为1,
在所给的正方形网格中,每个小正方形的边长均为1,