题目内容
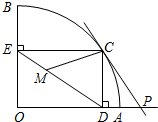
如图，扇形OAB，∠AOB=90°，⊙P与OA、OB分别相切于点F、E，并且与弧AB切于点C，则扇形OAB的面积与⊙P的面积比是 ．
【答案】分析：根据题意，构造直角三角形求得扇形的半径与圆的半径的关系，进而根据面积的求法求得扇形OAB的面积与⊙P的面积比．
解答：
解：连接OC，PE．
设PE为1，易得OP=
，那么OC=
+1．
∴扇形OAB的面积=
；
⊙P的面积=π，
∴扇形OAB的面积与⊙P的面积比是
．
点评：连接圆心和切点是常用的辅助线作法，本题的关键是求得扇形半径与圆半径之间的关系．
解答：
解：连接OC，PE．设PE为1，易得OP=
，那么OC=+1．∴扇形OAB的面积=
；⊙P的面积=π，
∴扇形OAB的面积与⊙P的面积比是
．点评：连接圆心和切点是常用的辅助线作法，本题的关键是求得扇形半径与圆半径之间的关系．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，扇形OAB是圆锥的侧面展开图，若小正方形方格的边长为1cm，则这个圆锥的底面半径为（ ）A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，扇形OAB的半径OA=r，圆心角∠AOB=90°，点C是
（2012•珠海三模）如图：扇形OAB的圆心角∠AOB=120°，半径OA=6cm，
如图，扇形OAB的圆心角为90°，分别以OA，OB为直径在扇形内作半圆，P和Q分别表示两个阴影部分的面积，那么P和Q的大小关系是（ ）
已知：如图，扇形OAB和扇形OA′B′的圆心角相同，设AA′=BB′=d．