题目内容
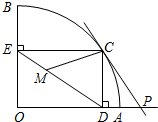 如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是 |
| AB |
(1)试说明:DM=
| 2 |
| 3 |
(2)试说明:直线CP是扇形OAB所在圆的切线.
分析:(1)连接OC,利用矩形的判定方法证明四边形EODC是矩形,即可得出答案;
(2)由∠CPO=∠CDE,∠NDO+∠EDC=90°,得出∠NOD+∠CPD=90°,即可证出.
(2)由∠CPO=∠CDE,∠NDO+∠EDC=90°,得出∠NOD+∠CPD=90°,即可证出.
解答: 解:(1)连接OC,
解:(1)连接OC,
∵∠AOB=90°,过点C作CD⊥OA于点D,作CE⊥OB于点E,
∴四边形EODC是矩形,
∵点M在DE上,DM=2EM,扇形OAB的半径OA=r,
∴OC=DE=r,
∴DM=
DE=
r;
(2)证明:∵四边形EODC是矩形,
∴ON=ND,
∴∠NOD=∠NDO,
∵∠CPO=∠CDE,∠NDO+∠EDC=90°,
∴∠NOD+∠CPD=90°,
∴直线CP是扇形OAB所在圆的切线.
 解:(1)连接OC,
解:(1)连接OC,∵∠AOB=90°,过点C作CD⊥OA于点D,作CE⊥OB于点E,
∴四边形EODC是矩形,
∵点M在DE上,DM=2EM,扇形OAB的半径OA=r,
∴OC=DE=r,
∴DM=
| 2 |
| 3 |
| 2 |
| 3 |
(2)证明:∵四边形EODC是矩形,
∴ON=ND,
∴∠NOD=∠NDO,
∵∠CPO=∠CDE,∠NDO+∠EDC=90°,
∴∠NOD+∠CPD=90°,
∴直线CP是扇形OAB所在圆的切线.
点评:此题主要考查了切线的判定与矩形的性质与判定,连接OC,利用矩形的对角线相等且互相平分是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是
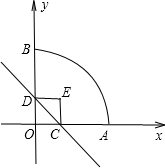
是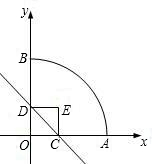 标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:
标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则: 是______;
是______; 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积. 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.
 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.