题目内容
 如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长为1cm,则这个圆锥的底面半径为( )
如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长为1cm,则这个圆锥的底面半径为( )A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:用“此扇形的弧长等于圆锥底面周长”作为相等关系,求圆锥的底面半径.
解答:解:设圆锥的底面半径为r,
则2πr=
,
所以r=
cm.
故选C.
则2πr=
90π2
| ||
| 180 |
所以r=
| ||
| 2 |
故选C.
点评:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•椒江区一模)我们把弧长等于半径的扇形叫等边扇形.如图,扇形OAB是等边扇形,设OA=R,下列结论中:①∠AOB=60°;②扇形的周长为3R;③扇形的面积为
(2013•椒江区一模)我们把弧长等于半径的扇形叫等边扇形.如图,扇形OAB是等边扇形,设OA=R,下列结论中:①∠AOB=60°;②扇形的周长为3R;③扇形的面积为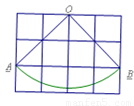
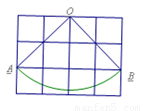
 ;④点A与半径OB中点的连线垂直OB;⑤设OA、OB的垂直平分线交于点P,以P为圆心,PA为半径作圆,则该圆一定会经过扇形的弧AB的中点.其中正确的个数为( )
;④点A与半径OB中点的连线垂直OB;⑤设OA、OB的垂直平分线交于点P,以P为圆心,PA为半径作圆,则该圆一定会经过扇形的弧AB的中点.其中正确的个数为( )
 ;④点A与半径OB中点的连线垂直OB;⑤设OA、OB的垂直平分线交于点P,以P为圆心,PA为半径作圆,则该圆一定会经过扇形的弧AB的中点.其中正确的个数为( )
;④点A与半径OB中点的连线垂直OB;⑤设OA、OB的垂直平分线交于点P,以P为圆心,PA为半径作圆,则该圆一定会经过扇形的弧AB的中点.其中正确的个数为( )