题目内容
12.我市正在积极开展“创建全国卫生城市”活动,某社区一超市看准商机,决定选购A、B两种品牌的杀虫剂销售,购进A种品牌的杀虫剂9件,B种品牌的杀虫剂10件,需要1810元;若购进A种品牌的杀虫剂12件,B种品牌的杀虫剂8件,需要1880元.(1)求A、B两种品牌的杀虫剂每件分别为多少元?
(2)若销售1件A型品牌的杀虫剂可获得45元,销售1件B品牌的杀虫剂可获得50元,根据市场需求,超市老师决定,购进B品牌的杀虫剂数量不超过12件,购进A品牌杀虫剂的数量要比购进B品牌的杀虫剂数量的2倍还多4件,这两种品牌的杀虫剂全部售出后,要使总的获利不少于1580元,问有几种进货方案?并写出这些方案.
分析 (1)直接利用“购进A种品牌的杀虫剂9件,B种品牌的杀虫剂10件,需要1810元;购进A种品牌的杀虫剂12件,B种品牌的杀虫剂8件,需要1880元”分别得出方程组求出答案;
(2)根据购进A品牌杀虫剂的数量要比购进B品牌的杀虫剂数量的2倍还多4件,要使总的获利不少于1580元,进而得出不等式求出答案.
解答 解:(1)设A品牌杀虫剂每件x元,B品牌杀虫剂每件y元,
由题意得:$\left\{\begin{array}{l}{9x+10y=1810}\\{12x+8y=1880}\end{array}\right.$,
解之得:$\left\{\begin{array}{l}{x=90}\\{y=100}\end{array}\right.$,
答:A品牌杀虫剂每件90元,B品牌杀虫剂每件100元;
(2)设购进B品牌杀虫剂a件,则A品牌杀虫剂购进(2a+4)件,
由题意得:45(2a+4)+50a≥1580,
解之得:a≥10,
又∵a≤12,
∵a为正整数,
∴a=10、11或12,
∴共有3种进货方案,
方案一:A品牌杀虫剂24箱,B品牌杀虫剂10箱;
方案二:A品牌杀虫剂26箱,B品牌杀虫剂11箱;
方案三:A品牌杀虫剂28箱,B品牌杀虫剂12箱.
点评 本题考查一元一次不等式组的应用以及二元一次方程组的应用,用不等式解答应用问题时,要注意对未知数的限制条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.∠AOB是平角,从点O引射线OC,使∠AOC:∠BOC=1:5,OD是∠BOC的角平分线,则∠COD的度数是( )
| A. | 50° | B. | 65° | C. | 70° | D. | 75° |
4.某商店购进一种商品,单价为30元试销中发现这种商品每天的销售量P(件)与每件的销售价x(元)满足P=100-3x.若商店在试销期间每天销售这种商品获得200元的利润,根据题意,下面所列方程正确的是( )
| A. | (x-30)(100-3x)=200 | B. | x(100-3x)=200 | C. | (30-x)(100-3x)=200 | D. | (x-30)(3x-100)=200 |
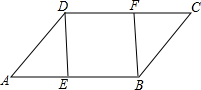 如图,在?ABCD中,点E,F分别在AB,CD上,AE=CF.
如图,在?ABCD中,点E,F分别在AB,CD上,AE=CF.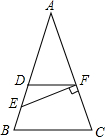 如图,等腰△ABC中,AB=AC,D是等腰AB上的一点,且AD=2DB,DF∥BC,E为DB的中点,若EF⊥AC,BC=6,则四边形DBCF的面积为15.
如图,等腰△ABC中,AB=AC,D是等腰AB上的一点,且AD=2DB,DF∥BC,E为DB的中点,若EF⊥AC,BC=6,则四边形DBCF的面积为15.