题目内容
7.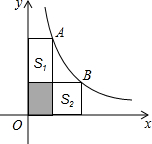 如图,点A、B是双曲线y=$\frac{2}{x}$上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=( )
如图,点A、B是双曲线y=$\frac{2}{x}$上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 欲求S1+S2,只要求出过A、B两点向x轴、y轴作垂线段求出与坐标轴所形成的矩形的面积即可,而矩形面积为双曲线y=$\frac{2}{x}$的系数k,由此即可求出S1+S2.
解答 解:∵点A、B是双曲线y=$\frac{2}{x}$上的点,分别经过A、B两点向x轴、y轴作垂线段,
则根据反比例函数的图象的性质得两个矩形的面积都等于|k|=4,
∴S1+S2=2+2-1×2=2.
故选:A.
点评 本题主要考查了反比例函数的图象和性质及任一点坐标的意义,有一定的难度.

练习册系列答案
相关题目
12.下列运算中,计算结果正确的是( )
| A. | x3+x3=x6 | B. | (3a)2×(3a-2)=1 | C. | (-a)3•a2=-a6 | D. | (-4m2n)2=16m4n2 |
19.下列计算正确的是( )
| A. | a2•a4=a8 | B. | a3÷a2=a | C. | 2x2+x2=2x4 | D. | (-2a2b)3=-6a5b3 |
16.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.下列各式求值正确的是( )
| A. | $\sqrt{{2}^{2}}=±2$ | B. | $±\sqrt{(-3)^{2}}=±3$ | C. | $-\sqrt{(-2)^{2}}=2$ |
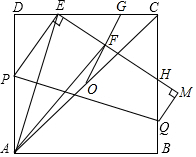 已知正方形ABCD,点P、Q分别是边AD、BC上的两动点,将四边形ABQP沿PQ折叠得到四边形EMQP,点E刚好落在CD边上,且DE=3,EF交BC于点H,连接AE,过点A作AF⊥EH于点F,取对角线AC的中点O,连接OF并延长交CD于点G,△ECH周长为18,则△EFG的周长为6+$\frac{3}{5}$$\sqrt{10}$.
已知正方形ABCD,点P、Q分别是边AD、BC上的两动点,将四边形ABQP沿PQ折叠得到四边形EMQP,点E刚好落在CD边上,且DE=3,EF交BC于点H,连接AE,过点A作AF⊥EH于点F,取对角线AC的中点O,连接OF并延长交CD于点G,△ECH周长为18,则△EFG的周长为6+$\frac{3}{5}$$\sqrt{10}$.