题目内容
18.已知AB=5、BC=12、AC=13,∠ABC=90°,则点B到AC的距离为$\frac{60}{13}$.分析 首先过B作BD⊥AC,再根据直角三角形的面积可得S△ACB=$\frac{1}{2}$AB•CB=$\frac{1}{2}$AC•BD,再代入数据可得答案.
解答  解:如图所示:
解:如图所示:
过B作BD⊥AC,
∵AB=5、BC=12,
∴S△ACB=$\frac{1}{2}$AB•CB=$\frac{1}{2}×$5×12=30,
∵S△ABC=$\frac{1}{2}$AC•BD=30,
∴BD=$\frac{60}{13}$,
故答案为:$\frac{60}{13}$.
点评 此题主要考查了三角形的面积以及点到直线的距离,关键是掌握直角三角形的面积公式.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
13.多项式-2x2-12xy2+8xy3的公因式是( )
| A. | 2xy | B. | 24x2y3 | C. | -2x | D. | 以上都不对 |
10.下列图案中是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.已知a,b是方程x2-x-3=0的两个实数根,则代数式a2-2a-b的值为( )
| A. | 1 | B. | -3 | C. | 3 | D. | 2 |
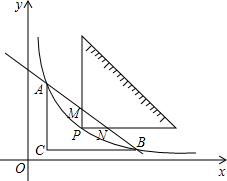 如图,将一块直角三角形纸板的直角顶点放在C(1,$\frac{1}{2}$)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+b与双曲线y=$\frac{4}{x}$的交点.
如图,将一块直角三角形纸板的直角顶点放在C(1,$\frac{1}{2}$)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+b与双曲线y=$\frac{4}{x}$的交点.