题目内容
8.已知a,b是方程x2-x-3=0的两个实数根,则代数式a2-2a-b的值为( )| A. | 1 | B. | -3 | C. | 3 | D. | 2 |
分析 先利用一元二次方程的解的定义得到a2=a+3,则a2-2a-b可变形为3-(a+b),然后利用根与系数的关系得到a+b=1,再利用整体代入的方法计算.
解答 解:∵a是方程x2-x-3=0的实数根,
∴a2-a-3=0,即a2=a+3,
∴a2-2a-b=a+3-2a-b=3-(a+b),
∵a,b是方程x2-x-3=0的两个实数根,
∴a+b=1,
∴a2-2a-b=3-1=2.
故选D.
点评 本题考查了根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了一元二次方程的解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
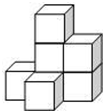 如图,若干个小正方体组成一个几何体.
如图,若干个小正方体组成一个几何体.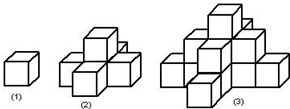
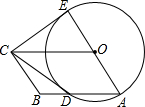 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线, 如图,将边长为8的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处,求:
如图,将边长为8的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处,求: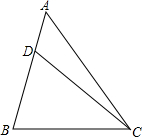 已知D是△ABC的边AB上一点,AD:DB=1:2,∠A=45°,∠BDC=60°,求证:△CBD∽△ABC.
已知D是△ABC的边AB上一点,AD:DB=1:2,∠A=45°,∠BDC=60°,求证:△CBD∽△ABC.