题目内容
9.已知3个不全为0的实数x、y、z,满足4x-y-5z=0和x+2y-8z=0,则分式$\frac{2{x}^{2}+3{y}^{2}+11{z}^{2}}{7{x}^{2}+8{y}^{2}+26{z}^{2}}$的值为$\frac{23}{63}$.分析 根据4x-y-5z=0和x+2y-8z=0,利用z分别表示x与y,然后将x与y代入原式即可求出答案.
解答 解:联立$\left\{\begin{array}{l}{4x-y=5z}\\{x+2y=8z}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=2z}\\{y=3z}\end{array}\right.$
∴原式=$\frac{2×(2z)^{2}+3×(3z)^{2}+11{z}^{2}}{7×(2z)^{2}+8×(3z)^{2}+26{z}^{2}}$
=$\frac{23}{63}$
故答案为:$\frac{23}{63}$
点评 本题考查分式的值,解题的关键是利用z分别表示出x与y,本题属于基础题型.

练习册系列答案
相关题目
19.下列运算正确的是( )
| A. | 3x+3y=6xy | B. | 19a2b-9ba2=10a2b | ||
| C. | 16a2-7a2=9 | D. | 3x+2x=5x2 |
20.为了了解全校七年级500名学生的视力情况,李老师从中抽查了60名学生的视力情况,针对这个问题,下面说法正确的是( )
| A. | 这个样本容量是60 | B. | 每名学生是个体 | ||
| C. | 60名学生是所抽取的一个样本 | D. | 500名学生是总体 |
17.先化简,再求值:$\frac{a}{a-b}$($\frac{1}{b}$-$\frac{1}{a}$)+$\frac{a-1}{b}$,其中a=-2,b=-3,则值为( )
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 3 |
4.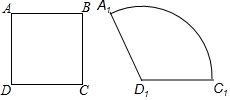 如图,用两根等长的金属丝,各自首尾相接,分别围成正方形ABCD和扇形A1D1C1,使A1D1=AD,正方形面积为P,扇形面积为Q,那么P和Q的关系是( )
如图,用两根等长的金属丝,各自首尾相接,分别围成正方形ABCD和扇形A1D1C1,使A1D1=AD,正方形面积为P,扇形面积为Q,那么P和Q的关系是( )
 如图,用两根等长的金属丝,各自首尾相接,分别围成正方形ABCD和扇形A1D1C1,使A1D1=AD,正方形面积为P,扇形面积为Q,那么P和Q的关系是( )
如图,用两根等长的金属丝,各自首尾相接,分别围成正方形ABCD和扇形A1D1C1,使A1D1=AD,正方形面积为P,扇形面积为Q,那么P和Q的关系是( )| A. | P<Q | B. | P=Q | C. | P>Q | D. | 无法确定 |
14.对于一次函数y=2-3x,下列命题是真命题的是( )
| A. | 函数值随自变量的增大而增大 | B. | 图象不经过第三象限 | ||
| C. | 向左平移2个单位后经过原点 | D. | 图象与x轴交于点(0,2) |
1.李克强总理在2017年政府工作报告中指出,扎实推进新型城镇化,深化户籍制度改革,今年实现进城落户1300万人以上,其中1300万用科学记数法表示为( )
| A. | 1.3×107 | B. | 1.3×106 | C. | 0.13×108 | D. | 1.3×108 |
18.一次函数y=(m-1)x+2的图象过点(-2,2),m的值是( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
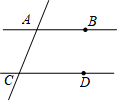 如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α-β,③β-α,④360°-α-β,∠AEC的度数可能是( )
如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α-β,③β-α,④360°-α-β,∠AEC的度数可能是( )